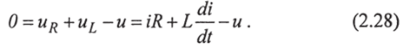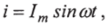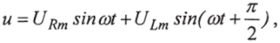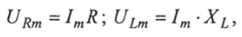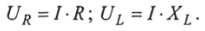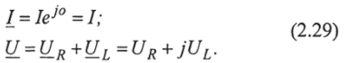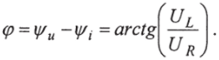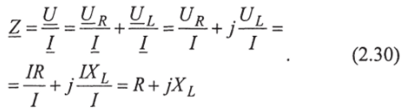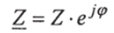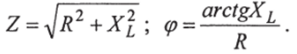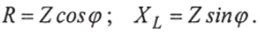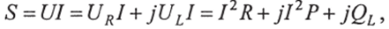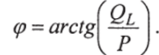Синусоидальный ток в электрической цепи с последовательным включением активного сопротивления (Я) и индуктивности (Ь)

На рис. 2.12 представлена электрическая цепь с последовательным включением активного сопротивления Я и индуктивности I, к которой приложено синусоидальное напряжение и.

Для электрической цепи (рис. 2.12а) в соответствии со вторым законом Кирхгофа справедливо выражение:

Принимая, что ток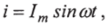

уравнение (2.28) с учетом фазовых соотношений перепишем:

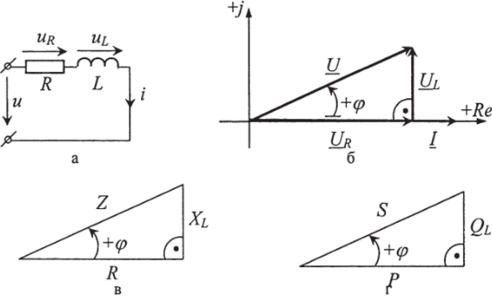
Рис. 2.12. Электрическая цепь с последовательным включением активного сопротивления и индуктивности (а); векторная диаграмма (б); треугольник сопротивлений (в); треугольник мощностей (г).

где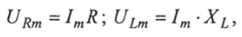

или для действующих значений:

Выражения для комплексного тока и напряжения цепи с учетом фазовых соотношений можно записать в виде:

При построении векторной диаграммы (рис. 2.126) за базовый вектор принимаем вектор тока /, направленный по положительной вещественной оси (+Яе). Вектор напряжения на сопротивлении Цн, согласно 2.29, совпадает по фазе с вектором тока /, а вектор напряжения на индуктивности (Уд опережает ток на 90°. Вектор приложенного напряжения Ц равен геометрической сумме векторов (Уд и (Уд. Угол (р на векторной диаграмме (рис. 2.126) равен.

Полное комплексное сопротивление цепи:

По этому уравнению построим треугольник сопротивлений (рис. 2.12в). При построении первоначально откладываем в масштабе (Ом/мм) отрезок Я, перпендикулярно к которому против часовой стрелки откладываем в масштабе отрезок Лх (умноженный на у). Диагональ полученного треугольника — отрезок 2 называется полным сопротивлением цепи.

Уравнение (2.30) можно переписать в показательной форме:

где.

Из треугольника сопротивлений связь между полным сопротивлением 2,11 и Лх можно записать:

Полная мощность цепи:

где? = III — полная мощность, В, А (вольт-ампер); Р — I² Я — активная мощность, Вт (ватт); Q_L = 1²Х? — индуктивная (реактивная) мощность, вар.

На рис. 2.12г построен треугольник мощности, в котором полная мощность 5 является диагональю треугольника. Угол (р определяется.

Связь между полной мощностью 5 и составляющими Р и 0,1 (рис. 2.12г):