Взаимодействие спроса и предложения на рынке. 
Рыночное равновесие

Предложение и спрос взаимосвязаны, они работают вместе и одновременно, подобно двум лезвиям ножниц (знаменитые «ножницы» Маршалла). Их взаимодействие (пересечение) устанавливает равновесную цену товара и объем его реализации. В результате достигается рыночное равновесие, означающее, что все рыночные факторы сбалансированны.

Покупатели и продавцы используют цены как сигналы, которые увязывают их желания, а затем происходит обмен денег на потребительские товары или факторы производства. Покупатели определяют цены спроса (или, иначе, тот максимум цепы, который они желают платить), а цены предложения устанавливают продавцы (или тот минимум, за который они готовы продать единицу своей продукции). При этом объем продаж будет равен объему спроса. Данное состояние получило название рыночного равновесия, которое наглядно представляется тремя способами: аналитическим, табличным и графическим.

Алгебраический пример иллюстрирует, как устанавливается равновесная цена. Предположим, что спрос и предложение заданы следующими уравнениями:

спрос Qd = Dp = 80 — 4р;

предложение Qs = Sp = -10 + 6p.

Равновесная цена устанавливается в точке, в которой объем спроса равен объему предложения: Dр = Sp, отсюда равенство спроса и предложения можно записать как 80 — 4р = -10 + 6р.

Решая уравнения относительно цены равновесия, получим р = 9.

Зная равновесную цену, можно найти равновесный объем спроса и предложения Q = Dp = Sp = 44.

Путем простого расчета можно убедиться, что никакого равновесного объема (Q) существовать не будет, если цена не будет равна 9.

Из данных табл. 5.4 видно, что только при цене 50 руб. спрос и предложение совпадают, следовательно, книжный рынок находится в состоянии равновесия.

График на рис. 5.6 иллюстрирует становление на конкурентном рынке равновесной цены (50 руб.) и равновесного объема реализации товара — 300 шт. (в точке Е пересекаются кривые спроса и предложения). В зоне, где цены выше равновесных (60 руб.), образуется избыток товаров, что постепенно снижает цены. В зоне, где цена ниже равновесной (40 руб.), образуется дефицит, который работает на повышение цен. В точке равновесной цены Е все, кто желает покупать, могут найти всех тех, кто желает продавать свои товары.

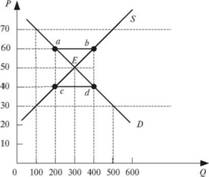
Рис. 5.6. Равновесие на книжном рынке Подобная ситуация реализуется в условиях совпадения цены равновесия с рыночной ценой. Однако их следует различать. Рыночная цена (ее часто называют действительной — реальной ценой) — это цена, которая действует в любой момент времени. Цена равновесия не меняется, пока не изменится соотношение между спросом и предложением, а рыночная цена может варьировать бесконечно. Поэтому равновесное состояние по своей природе нестабильно, так как рыночные условия, определяющие его, постоянно меняются, вызывая колебания спроса и предложения (табл. 5.5).

Таблица 5.5. Динамика спроса и предложения, ее влияние на изменение цен и объемов.

Когда рыночные цены выше равновесных, возникает избыток предложения — перепроизводство. Такой рынок называется рынком покупателя, поскольку он вынуждает продавцов снижать цены. По мере снижения цен объем спроса увеличивается, пока не достигает точки равновесия Е (см. рис. 5.6). При низких рыночных ценах возникает избыток спроса — дефицит и складывается рынок продавцов. Производитель легко реализует свою продукцию, после чего цены начинают расти, постепенно приближаясь к точке равновесия Е. Саморегуляцию рынка и восстановление равновесия (на прежнем или новом уровне) в свое время А. Смит описал как действие «невидимой руки». Именно механизм колебания спроса и предложения заставляет развиваться экономику, основанную на рыночных началах. Как правило, долгосрочные избытки или дефициты практически без исключения являются следствием государственного контроля над ценами.

Благодаря достижению равновесия цен и объемов продукции рынок распределяет ресурсы общества между различными вариантами их использования. Таким образом, посредством процесса взаимодействия спроса и предложения рынок отвечает на вопросы, как и для кого производить нужные товары и услуги.

Существует два подхода к проблеме экономического равновесия. Первый подход рассматривает сбалансированность каждого отдельного рынка (частное равновесие), второй — равновесие всей экономической системы как целого (общее равновесие). В данном случае мы рассматривали вопросы частного равновесия.