Способы устранения параметрического резонанса

Воспользуемся графиком, приведенным на рис. 7.4, чтобы наметить две принципиальные возможности устранения параметрического возбуждения. Первый путь связан с частотной отстройкой от критических зон, при которой значения ?2 в достаточной степени удаляются от ?2,. Второй путь проиллюстрирован на рис. 7.4 прямой е = е₂. Очевидно, если е₂ < е, где е, — критическое значение глубины пульсации, то прямая е₂ не пересекает ни одну из областей неустойчивости, а следовательно, независимо от частоты параметрического возбуждения система динамически устойчива на всем частотном диапазоне.

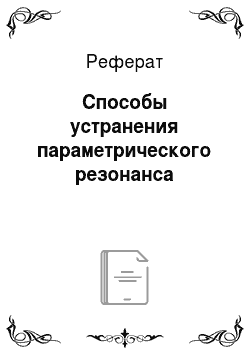
Для определения критического значения глубины пульсации воспользуемся энергетическим методом. Пусть однородное дифференциальное уравнение имеет вид уравнения (7.2), которое перепишем следующим образом:

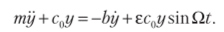
Как было показано в параграфе 5.13,.

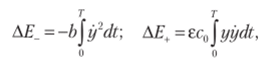
где ДЕ, AE_t — отведенная и подведенная энергии за один период колебаний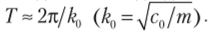

Приближенно примем в пределах одного периода колебаний у ~ A sin (k_nt + а), где А — усредненное значение амплитуды на этом периоде. Тогда в соответствии с (5.69).

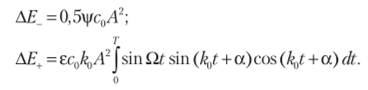
Пусть ?2 = ?2, = 2/г_(|, что отвечает главному параметрическому резонансу. При этом после интегрирования получаем АН = = 0,5ес_Г1/1-лс ().ч 2а. Максимуму подведенной энергии отвечает фазовый сдвиг, а = 0. Итак,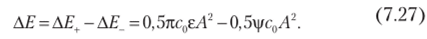

14 В Затуханию колебаний отвечает АЕ < 0. При этом на основании (7.27).

Таким образом, определенный уровень диссипативных сил служит своеобразным энергетическим барьером, препятствующим параметрическому возбуждению. Отношение г₄/г определяет запас устойчивости системы.

Подобным образом может быть также выявлена граница области динамической неустойчивости 8°. С этой целью примем Q. = Q. + Д?2. После аналогичных выкладок и некоторых упрощений получаем.

где v =.

При v —" 0 имеем 8° = 8, = |//л, что отвечает условию (7.28).

Если вместо линейной силы сопротивления на систему действует сила сухого трения Р, то согласно (5.70) АЕ = 4 IРIА и условие АЕ — АЕ < 0 при Q. =2k_{) принимает вид.

Э го означает, что при постоянной силе сопротивления существует критическое значение амплитуды Л", ниже которого обеспечиваются условия динамической устойчивости. При Л > А. в зоне главного параметрического резонанса амплитуды колебаний будут нарастать.

При нарушении условий динамической устойчивости амплитуды нарастают очень интенсивно. Поэтому даже кратковременное пребывание в критической зоне может привести к аварии. Отсюда следует, что для обеспечения безаварийной и надежной работы высокоскоростных механизмов реализация условия 8 < 8. более оправдана, чем частотная отстройка рабочих режимов от близких критических зон.

Чтобы лучше уяснить физическую сторону вопроса, рассмотрим в несколько упрощенной форме возбуждение параметрического резонанса на модели (рис. 7.5, а), которая состоит из невесомого жесткого стержня с массой т на конце, опирающегося на упругодиссипативный элемент (с₀,|/). Другой конец стержня шарнирно соединен с основанием, которое перемещается в горизонтальном направлении по закону х(?) = x₀sin Qt. При анализе малых колебаний стержня около положения равновесия в системе координат, жестко связанной с основанием, к массе т должна быть приложена переносная сила инерции F = —тх. Разложим силу Fua две составляющие F_t и F_N, как это показано на рис. 7.5, б, для каждой из четырех фаз колебаний. Поскольку F_f/ = Ftga ~ F //, дифференциальное уравнение малых колебаний имеет вид.

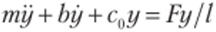
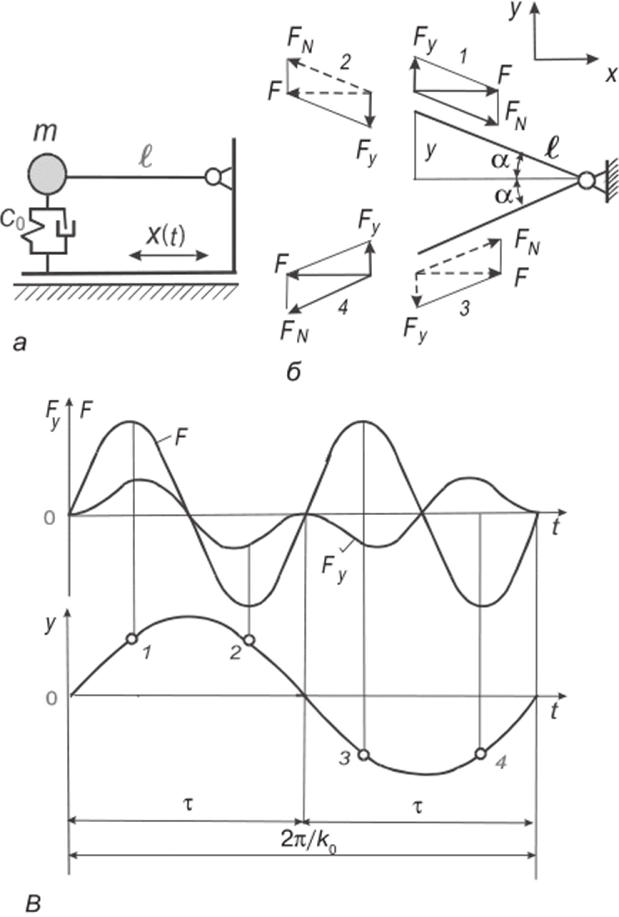
Рис. 7.5.

или после постановки Fих где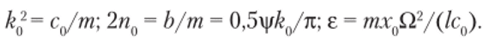

Заметим, что рассмотренный случай не имеет ничего общего с кинематическим возмущением, когда основание колеблется в вертикальном направлении, так как теперь сила F зави;

у

сит не только от времени, но и от у.

При Q ~ 2k_{0 У}у~Л sin Clt графики у (t), F (t), F (?) имеют вид, показанный на рис. 7.5, в. Легко убедиться в том, что для любой фазы колебаний направление силы F совпадает с направлением скорости колебаний у. Следовательно, эта сила стремится раскачать систему. С другой стороны, сила сопротивления всегда направлена против скорости у и стремится задемпфировать колебания. Результирующий эффект, связанный с этими двумя противоположными тенденциями, зависит от того, удовлетворяется ли условие (7.28). В нашем случае диссипация «побеждает» при.

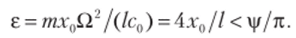
В заключение отметим одну характерную ошибку при анализе рассматриваемых систем. Основываясь на выражениях типа (7.25), нередко возникает заманчивое предположение, нельзя ли при малой глубине пульсации (но сравнению с единицей) заменить переменную частоту k (t) ее средним значением k₀, что, разумеется, привело бы к существенному упрощению задачи. Однако в данном случае за подобное «осреднение» можно очень дорого расплатиться, поскольку при этом игнорируется возможность нарушения условия? < е₄ и связанная с этим возможность параметрического резонанса.