Остойчивость, непотопляемость и спуск судна на воду

Начальная остойчивость

Остойчивостью называют способность судна, выведенного из положения равновесия, возвращаться в него после прекращения действия внешних сил.

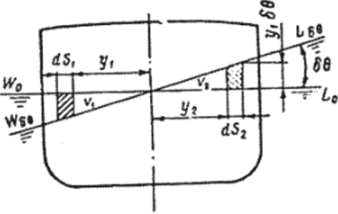
Рис. 2.1. Равнообъемное наклонение.

Как видно из определения, между понятиями остойчивость судна и устойчивость, а также устойчивое равновесие тела в механике заметна аналогия. Однако имеются и отличия: в остойчивости рассматриваются не только бесконечно малые, но и конечные отклонения от положения равновесия; устойчивость — чисто качественное состояние, а остойчивость имеет меру, наконец, судно может либо обладать остойчивостью (устойчивое равновесие), либо быть неостойчивым (иметь неустойчивое и безразличное равновесие).

Плавающее судно как твердое тело обладает шестью степенями свободы, следовательно можно говорить об отклонениях от положения равновесия, но всем этим степеням. Что касается поступательных перемещений вдоль осей ох и оу, а также вращательного относительно оси ог, то им ничто не препятствует, поэтому не возникает восстанавливающих сил и момента. Таким образом, по отношению к этим отклонениям судно не обладает остойчивостью, а положение равновесия здесь безразличное. Это обстоятельство не грозит судну гибелью, не препятствует его использованию по назначению.

Отклонение вдоль вертикальной оси oz приводит к появлению (для судна, имеющего запас плавучести) восстанавливающих сил, т. е. такое судно всегда обладает вертикальной остойчивостью. Кроме того, судно должно сопротивляться, противостоять, наклонениям относительно осей ох и оу, в противном случае оно опрокинется, перевернется. Устойчивое равновесие при указанных наклонениях не обеспечивается автоматически, как это было с вертикальной остойчивостью, а требует определенных конструктивных решений. В общем случае характер равновесия зависит от формы корпуса, распределения нагрузки, величины отклонения и т. д. Изучением всех этих вопросов и занимается «статическая остойчивость» (или просто «остойчивость»). В зависимости от того, в какой плоскости происходит наклонение, различают поперечную остойчивость — поворот судна относительно оси ох, сопровождаемый появлением угла крена, и продольную остойчивость — вокруг оси оу, угол дифферента.

Кроме того, выделяют начальную остойчивость, когда углы наклонения малы, и остойчивость на больших углах крена. В первом разделе удается получить простые аналитические зависимости, определяющие остойчивость судна, второй раздел имеет более общий характер и включает в себя начальную остойчивость как частный случай.

Статическая остойчивость предполагает, что силы или моменты прилагаются к судну в течение достаточно длительного промежутка времени. Если эти условия не соблюдаются и силами инерции пренебрегать нельзя, то вступают в действие законы динамической остойчивости.

Будем рассматривать равнообъемные наклонения, когда угловые перемещения происходят в условиях вертикального равновесия, т. е. при соблюдении закона Архимеда. Такое возможно, если к судну приложен чистый момент, например, когда груз перемещен с одного борта на другой. Любой более сложный вариант, вызывающий наклонение судна, может рассматриваться как сумма простых, включающих в том числе и чистый момент.

Проанализируем равнообъемное наклонение судна в поперечной плоскости на бесконечно малый угол 50 (рис. 2.1). Поскольку нас интересует положение корпуса относительно поверхности воды, можно его поворот вокруг оси ох заменить эквивалентным поворотом действующей ватерлинии, как это сделано на рис. 2.1. Этот же прием будем использовать и в дальнейшем при изучении поперечной остойчивости.

Так как наклонение равнообъемное, то объемы вошедшего в воду и вышедшего из нее клиньев одинаковы:

В свою очередь, можно записать (см. рис. 2.1):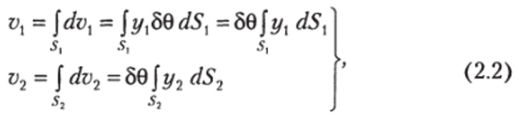

где.

— объем элементарной призмы с основанием dS. и высотой г/50; 50 — угол наклонения; dS. и у, — элементарная площадка и ее отстояние от оси наклонения соответственно. Сопоставляя (2.1) и (2.2), находим.

Интегралы в (2.4) суть статические моменты площадей и 5, и 5₂ относительно оси поворота, т. е.

откуда следует, что эта ось центральная, т. е. проходит через центр тяжести площади ватерлинии.

Этот вывод можно сформулировать несколько иначе: две равнообъемные ватерлинии пересекаются по линии, проходящей через их общий центр тяжести. Доказанное для равнообъемных наклонений положение называется теоремой Эйлера и справедливо для малых наклонений относительно любой оси, т. е. и для дифферента судна.