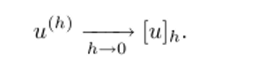Сходимость разностной схемы

Если для дифференциальной задачи составлена разностная схема и получено ее решение — сеточная функция, то возникают два вопроса:

соответствует ли решение разностной задачи точному решению дифференциальной задачи?

— если такое соответствие имеется, то можно ли повысить точность приближенного решения измельчением сетки?

Поставленные вопросы тесно связаны с понятием сходимости разностного решения к точному решению дифференциальной задачи, которое является основным для разностных схем.

Обозначим через [u]h проекцию на сетку точного решения дифференциальной задачи. Условие сходимости можно записать с помощью выше введенных обозначений так:

Дадим определение сходимости разностной схемы. Решение и^ разностной краевой задачи при h. —> 0 (измельчении сетки) сходится к решению и дифференциальной краевой задачи, если ||[гф, — -" ||-0 при h —> 0. Если сверх того выполняется неравенство ПН, — и^|| ^ Ch^k, то говорят, что имеет место сходимость порядка h^k или разностная схема имеет кй порядок сходимости.

Сходимость является фундаментальным требованием, предъявляемым к разностной схеме для численного решения дифференциальной краевой задачи. Если сходимость имеет место, то с помощью разностной схемы можно вычислить решение с любой наперед заданной точностью, выбирая для этого h достаточно малым.

Приведенное определение не указывает на способ построения сходящейся разностной схемы. Мы видели из примеров предыдущего раздела, что для одной задачи можно составить несколько разностных схем, но вопрос о том, какая из них обеспечит сходимость, остается открытым.

Непосредственно установить сходимость в общем случае не представляется возможным, но для линейных задач она может быть установлена на основании других, более простых для проверки свойств разностной схемы: аппроксимации и устойчивости.