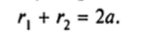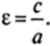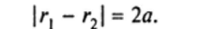Линии второго порядка
Где, а и b — полуоси эллипса, Ь2 = а2 — с2, точка О (0, 0) — центр эллипса, с — половина расстояния между фокусами эллипса. Из уравнения (8.29) следует, что оси эллипса являются осями его симметрии, а точка их пересечения — центром его симметрии. График параболы показан на рис. 8.20. Нетрудно видеть, что перемена осей координат приводит к более привычным по курсу школьной математики уравнениям… Читать ещё >
Линии второго порядка (реферат, курсовая, диплом, контрольная)
Рассмотрим три наиболее используемых вида линий: эллипс, гиперболу и параболу.
Линия, для всех точек которой сумма расстояний от двух данных точек, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами, называется эллипсом.
Согласно определению эллипса сумма расстояний от произвольной точки М на этой линии до его фокусов У7, и F2 постоянна (рис. 8.18).
Отсюда можно вывести уравнение эллипса в его основной {канонической) форме.
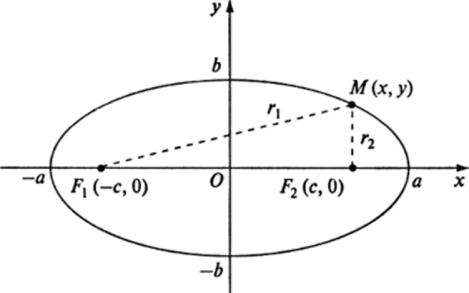
Рис. 8.18.
где а и b — полуоси эллипса, Ь2 = а2 — с2, точка О (0, 0) — центр эллипса, с — половина расстояния между фокусами эллипса. Из уравнения (8.29) следует, что оси эллипса являются осями его симметрии, а точка их пересечения — центром его симметрии.
В частном случае, когда а = Ь> фокусы эллипса сливаются, с = 0 и мы имеем окружность радиуса а с центром в начале координат.
Характеристикой эллипса, показывающей меру его вытянутости, является эксцентриситет — величина, определяемая отношением.
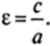
Гиперболой называется линия, для всех точек которой модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
На рисунке 8.19 показаны все основные элементы гиперболы. Разность расстояний от произвольной точки М на гиперболе до фокусов h и F2 согласно определению есть величина постоянная.
И з этой основной предпосылки выводится каноническое уравнение гиперболы, которое имеет вид:
где Ь2 = с2 — а2.
Нетрудно видеть, что прямые у = ±-х являются наклонными асимптота;
а
ми гиперболы. Эта линия имеет две оси симметрии, точка пересечения которых является центром симметрии гиперболы.
Параболой называется линия, все точки которой находятся на одинаковом расстоянии отданной точки, называемой фокусом, и отданной прямой, называемой директрисой и нс проходящей через фокус.
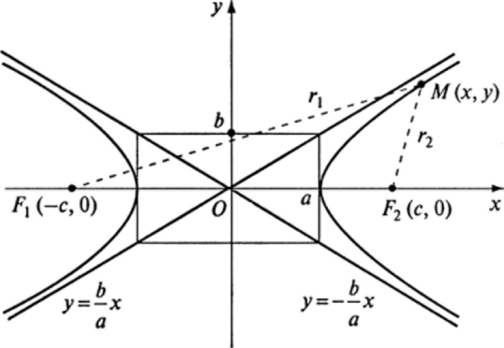
Рис. 8.19.
Согласно определению точка Л/ (х, у) лежит на параболе, если г, = г2. Отсюда и выводится каноническое уравнение параболы, которое имеет вид:
График параболы показан на рис. 8.20. Нетрудно видеть, что перемена осей координат приводит к более привычным по курсу школьной математики уравнениям параболы вида у = Ах2, где А — постоянное число.
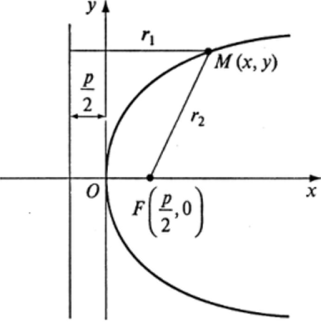
Рис. 8.20.