Субгармонический резонанс. 
Динамика машин. 
Колебания

Помимо рассмотренных режимов вынужденных колебаний в нелинейных системах возможно возбуждение субгармонических резонансов, частота которых равна со//, где / > 1 — целое число. Происхождение этих режимов связано с влиянием высших гармоник нелинейной функции U (q°, q^{)), которые ранее при использовании разложения (8.10) были отброшены.

Возможность возникновения этих режимов покажем на примере. Как было показано в параграфе 5.13, любой резонансный режим можно рассматривать как «незатухающие» свободные колебания при условии, что отрицательная работа сил сопротивления компенсируется работой вынуждающей силы на данном режиме. Для математического описания подобных режимов воспользуемся уравнением (8.20), приняв п₀ = 0 и V_{ = 0. Свободные колебания будем искать в виде.

Напомним, что ранее, при изложении метода гармонической линеаризации (см. параграф 8.3), мы сохранили лишь основную гармонику, а высшими гармониками пренебрегли. Далее, используя тождество cos⁵ kt = 0,75 cos kt + 0,25 cos 3kt, подставим при приведенных выше допущениях предполагаемое решение (8.26) в уравнение (8.20) и сгруппируем члены при cos kt и cos3kt. Поскольку коэффициенты при этих функциях при свободных колебаниях обращаются в нуль, получаем следующую систему алгебраических уравнений:

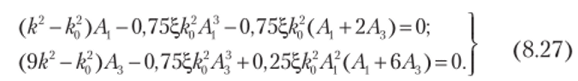
Примем, что, а = Aj/Л, 1. Тогда из первого уравнения системы (8.27) следует, что k.,(A) = k^( 1 + 0,75ЗД²), причем этот результат полностью совпадает с формулой (8.22), полученной методом гармонической линеаризации. (Заметим, что на основании точного решения, которое выражается через эллиптические функции, можно показать, что, а < 0,045 [ 1 ]). При малых значениях а, согласно второму уравнению системы (8.27), имеем.

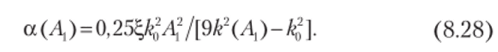
Далее обратимся к анализу вынужденных колебаний. Пусть гармоническая вынуждающая сила имеет вид f. cos (Q (t) + у) • Возникает вопрос, при каких условиях эта сила может возбудить резонансные колебания па частоте со = Q/j, где j — целое число. Для определенности ниже примем j = 3, что согласно принятой терминологии соответствует субгармоническому резонансу порядка 1/3. Сначала определим величину рассеянной энергии за один период колебаний 2я/со при амплитуде, равной Л: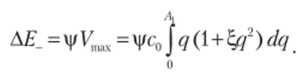

Здесь i — коэффициент рассеяния; У_тах — максимальное значение потенциальной энергии; с₀ = ak₀² — коэффициент жесткости при q —> 0; а — инерционный коэффициент.

После интегрирования имеем

Эта отведенная из механической системы энергия должна компенсироваться работой вынуждающей силы, которая согласно (5.68) в нашем случае определяется как.

Принимая 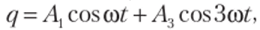после подстановки в.

(8.30) и интегрировании получаем.

Как уже отмечалось, резонансный режим соответствует поддержанным вынуждающей силой свободным колебаниям, поэтому соотношение между А₃ и Л, определяется формулой (8.28), т. е. как Л₃ = а (Л,)Л_г При этом условие существования субгармонического резонанса может быть записано следующим образом: АЕ < (АЕ₊)_тах. Отсюда, используя (8.29) и (8.31), окончательно имеем.

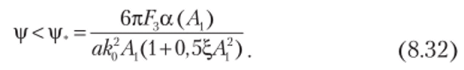
Амплитуде A_t на амплитудно-частотной характеристике соответствует точка скелетной кривой. При этом.

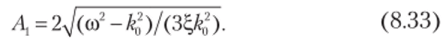
Максимальная амплитуда Л, отвечающая условию (8.32), соответствует наибольшему отводу энергии.

Для амплитуды Л, существует также граница снизу, так как при малых значениях, А система приближается к линейной, поскольку согласно (8.31) и (8.28) при этом быстро уменьшается амплитуда третьей гармоники, а следовательно, и работа вынуждающей силы [1].

В предельном случае при ^ = 0, что соответствует линейной системе, функция, а (Л,) согласно (8.28) обращается в нуль, а следовательно, условие (8.32) не может быть выполнено, и субгармонические резонансы нс возникают.

Итак, субгармонические резонансы обычно возникают при сочетании сильных нелинейностей и слабой диссипации.

Для исключения возможности возбуждения субгармонического резонанса порядка 1/3 при рассмотренной кубичной нелинейности должно с некоторым запасом удовлетворяться условие у > j/. 11а рис. 8.5 в качестве иллюстрации приведены результаты компьютерного моделирования при ^ = 0,5, / = 0,063 и |/,= 0,15. Сопоставление графиков q (t) и F (t) свидетельствует о трехкратном уменьшении частоты вынужденных колебаний по сравнению с частотой вынуждающей силы.

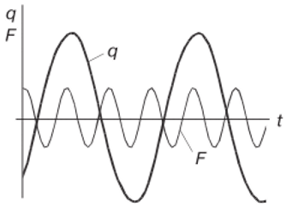
Рис. 8.5.