Обобщение формулы Эйлера

Рассмотрим стержень длиной /, один конец которого закреплен жестко, а на другом свободном конце приложена центральная сжимающая сила F (рис. 15.8).

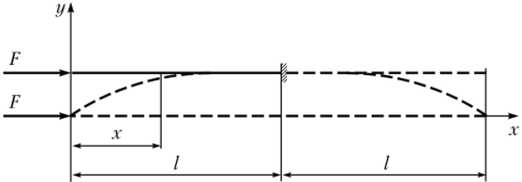
Рис. 15.8. К обобщению формулы Эйлера Общее решение задачи, записанное в виде формулы (15.15), в этом случае остается в силе. Что же касается граничных условий, то они запишутся в следующем виде:

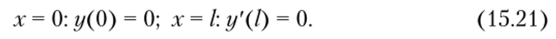
Искомое решение можно найти и иначе. Условно продолжим стержень вправо от защемленной опоры на длину / симметрично левой части, и тогда вместо граничных условий (15.21), получим новые условия:

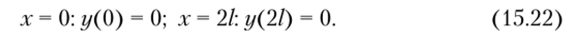
Таким образом, новая задача фактически совпала с рассмотренной выше задачей Эйлера. Различие состоит только в том, что в конечном результате (15.20) длину / следует заменить на 21:

Формулу Эйлера можно обобщить также на другие случаи закрепления концов стержня. Для этого в расчетную формулу Эйлера вводится поправочный коэффициент р, называемый коэффициентом приведения длины стержня:

Коэффициент численно равен обратному числу от количества полуволн синусоиды, укладывающихся вдоль изогнутой оси стержня. На рис. 15.9 представлены различные виды крепления концов стержня и соответствующие им коэффициенты приведения длины.

Можно показать, что для первых трех стержней, изображенных на рис. 15.9, а — в, значения коэффициента приведенной длины точное. Что же касается четвертой задачи, то для нее значение приведенной длины определено приближенно. Рассмотрим задачу определения р для этого случая (рис. 15.9, г).

Уравнение деформированной оси стержня имеет вид.

Здесь R — величина горизонтальной реактивной силы верхней опоры.

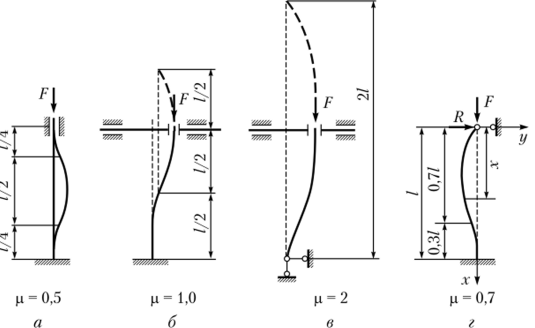
Рис. 15.9. Значение коэффициента приведения длины при различных условиях закрепления стержня

После преобразования уравнения (15.25) с учетом формулы (15.13) получим.

Уравнение (15.26), в отличие от уравнения (15.14), является неоднородным. Его общее решение запишется так же, как и общее решение соответствующего однородного уравнения (15.14). Частное решение имеет вид.

Таким образом, решение уравнение (15.25) запишется в форме.

В этом решении величина R играет роль третьей неизвестной константы, п поэтому для решения этой задачи необходимо сформулировать третье граничное условие:

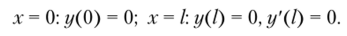
Используя граничные условия, получим систему трех нелинейных уравнений.

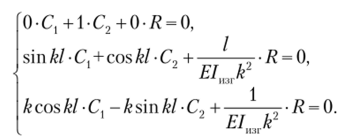
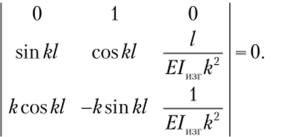
Раскрывая определитель, приходим к следующему нелинейному уравнению:

Решение нелинейного уравнения (15.29) можно получить как численно, так и графически. Для наглядности выберем второй способ решения. Построим графики следующих функций: у = tgkl, у = kl (рис. 15.10).

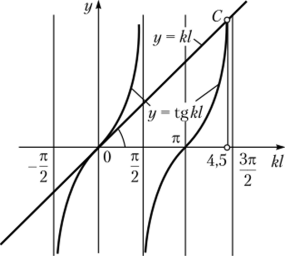
Рис. 15.10. Графики функций у = tg kl, у = kl.

Точка пересечения графиков С соответствует значению корня kl ~ 4,5, откуда.

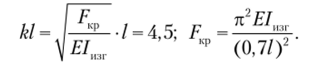
В формулу для критической силы входит главный центральный момент инерции относительно оси Oz — /_Ю1. = так как мы загодя сделали предположение о том, что стержень теряет устойчивость и изгибается в направлении, перпендикулярном к оси Ох. Однако, как уже отмечалось, если при этом условия закрепления опор позволяют стержню деформироваться в любом направлении равновероятно, то стержень потеряет устойчивость в том направлении, в котором момент инерции его поперечного сечения имеет минимальное значение 7_min.

Если же условия закрепления более сложные, то для оценки критической силы необходим дополнительный анализ. Для примера рассмотрим стержень (рис. 15.11), левая опора которого жестко заделана. Что касается правой опоры, то здесь заданы условия подвижной заделки, разрешающей перемещения и повороты в плоскости ху и запрещающие их в плоскости zx. Поперечное сечение стержня — прямоугольное с отношением сторон Н = 2В.

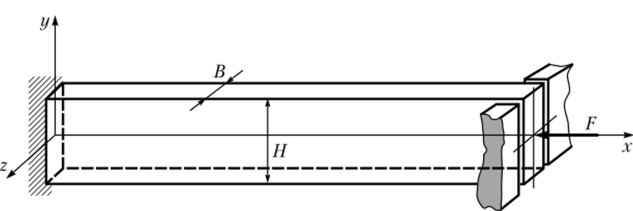
Рис. 15.11. Стержень с жестко заделанной левой опорой

Закреплению стержня в плоскости ху соответствует коэффициент приведения длины р = 2 (см. рис. 15.8), а в плоскости xz — р = 0,5 (см. рис. 15.9, а).

Подсчитаем критические силы в предположении о том, что потеря устойчивости произойдет: 1) в плоскости ху и 2) в плоскости xz:

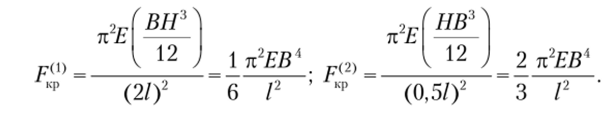
Сравнивая значения, заключаем: потеря устойчивости произойдет в плоскости ху, поскольку этому варианту соответствует меньшее значение критической силы.