Точечные оценки параметров распределения случайных величин и отклонений

Вероятностные характеристики погрешностей измерения определяются, как правило, на основании экспериментальных данных методами математической статистики. Иногда для этого проводят специальные эксперименты с целью аттестации средств измерения, иногда они совмещены с измерениями контролируемого параметра. При этом оцениваются математическое ожидание и среднее квадратичное отклонение.

Оценка вероятностной характеристики погрешностей измерения называется точечной, если она выражена одним числом. Любая точечная оценка, вычисленная на основании опытных данных, является случайной величиной. При этом функция ее распределения зависит от распределения случайной величины и числа опытов п.

Точечная оценка называется несмещенной, если ее математическое ожидание совпадает с истинным значением оцениваемого параметра.

Точечная оценка называется состоятельной, если при увеличении количества наблюдений (объема выборки) ее отличие от оцениваемого параметра может быть сколь угодно малым.

Точечная оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра.

Каждое из этих понятий характеризует качество точечных оценок. При прочих равных условиях лучшей будет та оценка, которая имеет, например, наименьшее смешение. Среди всех нормально распределенных оценок наилучшей будет несмещенная эффективная оценка.

Теоретическим обоснованием возможности экспериментального определения вероятностных характеристик является закон больших чисел, который для случайных величин формулируется следующим образом.

Пусть проведена серия и одинаковых независимых экспериментов по наблюдению за случайной величиной X, имеющей конечные М (х) и /)(а).

Обозначим через X среднее арифметическое результатов наблюдений.

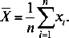
В соответствии с законом больших чисел для любых сколь угодно малых? и, а всегда найдется такое при котором в случае п > и, ь4.

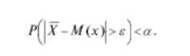
Среднее арифметическое результатов наблюдений является несмещенной оценкой математического ожидания случайной величины, а следовательно, ее истинное значение совпадаете математическим ожиданием случайной величины:

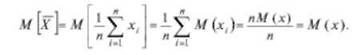
Так как среднее арифметическое результатов измерений получено X в результате сложения случайных величин -, то оно также является п случайной величиной с дисперсией В (х). Значение дисперсии среднего значения можно определить следующим образом:

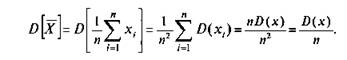
Из выражения (5.56) следует, что точность результата измерения можно повысить при увеличении числа измерений. Дисперсия среднего арифметического из п наблюдений в п раз меньше дисперсии результата однократного наблюдения.

Среднее квадратичное отклонение среднего арифметического определяется по формуле.

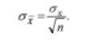
При п ->со од. стремится к нулю. Эго означает, что среднее арифметическое ряда измерений сходится по вероятности к математическому ожиданию и является его состоятельной оценкой.

Среднее арифметическое значение является также и эффективной оценкой математического ожидания, т. е. имеет минимальную дисперсию, равную ?1¹.

Рассмотрим пример определения среднего арифметического на основании изменяющегося числа наблюдений.

На рис. 5.13 представлен график зависимости результатов наблюдений (ряд I — отклонения размера в /'-ом опыте, ряд 2 — среднее арифметическое результатов последовательных измерений. Значения этого ряда получаются следующим образом. Первое значение.

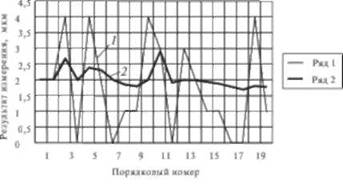
Рис. 5.13. Зависимость результатов наблюдений от числа наблюдений.

равно первому значению из ряда I, второе значение равно сумме первого и второго значений ряда I, деленное на 2, третье значение равно сумме первого, второго и третьего значений первого ряда деленное на 3, и т. д. Последнее значение второго ряда равноV х. В данном примере п = 20).

Среднее из 20 наблюдений А1 =1,75 мкм служит точечной оценкой истинного отклонения измеряемой величины.

Результаты отдельных измерений, как это следует из графика, имеют достаточно большой разброс относительно среднего арифметического (ряд I), а разброс отдельных средних арифметических значительно меньше (ряд 2). Он уменьшается по мере увеличения числа измерений.

В качестве точечной оценки дисперсии выбирают среднее значение квадрата отклонения случайной величины от среднего значения.

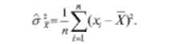
Эта оценка является состоятельной, но смешенной, так как ее математическое ожидание равно.

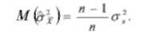
В связи с этим точечную оценку дисперсии принято определять по формуле:

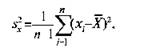
где 5; - эмпирическая дисперсия.

Точечная оценка среднего квадратичного отклонения определяется из выражения.

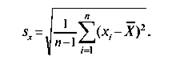
Величина^{характеризует} разброс отдельных результатов измерения относительно среднего арифметического значения X.

В литературе величину ах называют средним квадратичным, или стандартным отклонением генеральной совокупности, а л — выборочным средним квадратичным отклонением.

Среднее арифметическое X имеет дисперсию, в п раз меньшую, чем дисперсия случайной погрешности (5.57). В связи с этим в качестве точечной оценки дисперсии среднего арифметического принимается выражение.

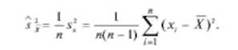
Оценка среднего квадратичного отклонения среднего арифметического соответственно равна.

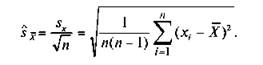
С помощью полученных оценок Л' и .^результат измерения, например длины, записывается следующим образом:

что позволяет сделать соответствующие выводы относительно точности измерения: число измерений п характеризует надежность определения л*" а величина л;(характеризует близость А1 к истинному значению Л.