Определение площадей участков по результатам полевых измерений

Аналитический способ

Площади участков по результатам полевых измерений определяют следующим образом. Вначале на местности выполняют необходимые измерения (например, прокладывают теодолитный ход), по результатам которых вычисляют прямоугольные координаты вершин участка.

Формулы для вычисления площади участка по координатам его вершин вытекают из рисунка 4.1, на котором участок имеет форму треугольника (для простоты), и его вершины пронумерованы по ходу часовой стрелки (от направления нумерации зависит вид формулы).

Площадь S треугольника можно представить как сумму площадей S₁ и S₂ двух трапеций, составленных на сторонах треугольника 1−2 и 2−3 перпендикулярами на ось У, без площади S₃ аналогичной трапеции на стороне 3−1.

Удвоенная площадь трапеции равна произведению ее высоты на сумму оснований:

• 2S = (X₁ + X₂) (Y₂ — Y₁) + (X₂ + X₃) (Y₃ — Y₂) — (X₁ + X₃) (Y₃ — Y₁).
• 2S = X₂(Y₂ — Y₃) + X₂ (Y₃ — Y₁) + X₃(Y₁ — Y₂).

Удвоенная площадь участка равна сумме произведений ординаты (Y) каждой вершины на разность абсцисс (Х) предыдущей и последующей его вершин.

Для многоугольника с числом вершин n, пронумерованных по ходу часовой стрелки, формулы площади будут иметь вид.

В целях контроля площадь участка вычисляют по обеим формулам. Кроме того, промежуточный контроль выполняется по приведенным ниже формулам.

Для вычисления площади участка по координатам Х_i, Y_i его вершин или по приращениям координат ДХ_i, ДY_i можно использовать также следующие формулы:

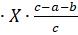
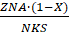
Относительная погрешность определения площади аналитическим способом зависит от точности определения координат вершин участка и приблизительно равна удвоенной относительной погрешности измерения линий. Например, при измерении линий лентой (средняя точность порядка 1:2000) относительная погрешностъ определения площади составляет около 1:1000.

Средняя квадратическая погрешность площади участка с n вершинами.

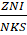
где m_X = m_Y = m_{X, Y} — средняя квадратическая погрешность определения координат вершин участка;

D_i — расстояние от начала координат до i-й вершины участка (в частном случае — от одной из вершин, принятой за начало координат).

Для прямоугольника со сторонами а и b погрешность площади Если приведенные для m_S формулы решать относительно m _{Х, У}, то по заданной погрешности определения площади m_S можно рассчитать необходимую точность определения координат m _{Х, У} вершин земельного участка, на основании которой — и необходимую точность угловых и линейных измерений.

Среднюю квадратическую погрешность площади земельного участка можно вычислить также по формуле.

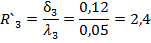
где m_t = m_{X, Y}v2 — средняя квадратическая погрешность положения вершин или измерения сторон участка,.

k — коэффициент вытянутости (отношение длины к ширине участка, для треугольника — отношение высоты к основанию).

Подкоренное выражение имеет минимум при k = 1, то есть наиболее то-чно определяется площадь квадратного участка или треугольника, в котором высота равна основанию.

В том случае, когда используются координаты пунктов в проекции Гаусса-Крюгера (на плоскости), а также топографические карты, составленные в той же проекции, то вычисленные площади S_пр будут больше их горизонтальных проложений S_r. Для приведения полученной площади к горизонтальной проекции используют формулу.

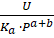
где Y_m — средняя ордината участка (расстояние от осевого меридиана до середины участка).

Площадь участка на физической поверхности Земли S_ф больше площади горизонтальной проекции S_r ввиду наклона местности. Для получения площади физической поверхности участка его разбивают на части с одинаковыми продольными поперечными наклонами, определяют их углы наклона соответственно v_пр, v _пп, а площадь каждой из них вычисляют по очевидной формуле.

Если для определения площадей используются координаты пунктов государственной геодезической сети, которые относятся к референц-эллипсоиду, а не к поверхности Земли, то вычисленные площади S₀ будут несколько преуменьшены. Для получения площади S на поверхности Земли используют формулу.

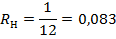
где Н — средняя высота участка;

R — средний радиус Земли, равный 6371 км.

Геометрический способ

Способ основан на делении участка на простейшие геометрические фигуры, чаще всего треугольники и четырехугольники, со сторонами в виде прямых линий, удобных для измерения (рисунок 4.2).

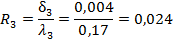
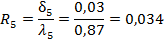
а) б) в) г).

Рисунок 4.2 — Схемы измерений в простейших фигур для определения площади:

а, б, в — треугольника, г — четырехугольника В фигурах измеряют соответствующие элементы (стороны, углы) и по известным формулам геометрии вычисляют площадь каждой из них, а площадь участка находят как сумму площадей составляющих его фигур. Для определения площади треугольника можно измерить: две стороны D₁, и D₂ и угол между ними в (рисунок 4.2, а); одну сторону D и прилегающие к ней углы в₁ и в₂ (рисунок 4.2, б); все три стороны D₁, D₂, D_з (рисунок 4.2, в). Площади треугольников будут равны соответственно:

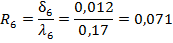
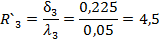
Где.

P = (D₁ + D₂ + D₃) / 2;

полупериметр треугольника.