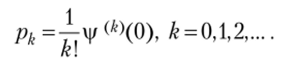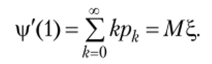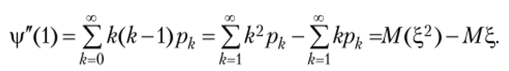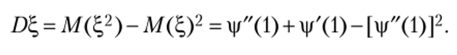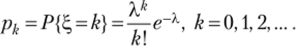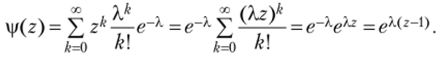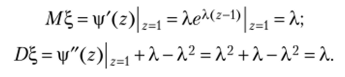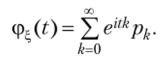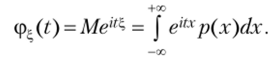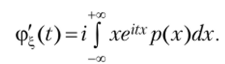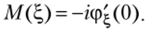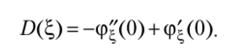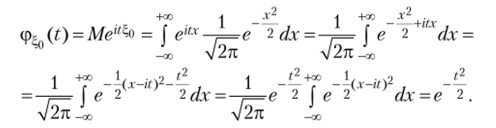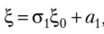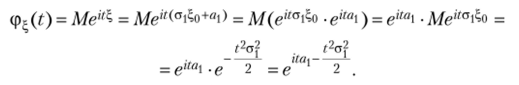Производящие и характеристические функции

Вместо ряда распределения или функции распределения для описания случайной величины часто применяют производящие и характеристические функции. Пользуясь ими, можно упростить расчет числовых характеристик случайных величин, а также упростить задачу нахождения закона распределения суммы нескольких независимых случайных величин.

Пусть ?, — целочисленная СВ, принимающая в зависимости от случайного исхода со одно из значений 0, 1,2, … с соответствующими вероятностями p_k = Р{^ = k}, k = 0, 1, 2, … .

Определение 3.28. Производящей функцией целочисленной случайной величины? называется функция.

Можно считать, в зависимости от удобства, производящую функцию функцией комплексной или действительеной переменной.

Ясно, что распределение вероятностей случайной величины ?, однозначно определяется ее производящей функцией 4/(2).

По формуле Тейлора.

Производящая функция цj (z) при фиксированном z представляет собой не что иное, как математическое ожидание случайной величины g (?) = z^:

Дифференцируя правую и левую части формулы (3.9) (или (3.10)) по 2 и полагая 2=1, получим.

Дифференцируя по 2 дважды и полагая 2=1, будем иметь.

Тогда для дисперсии случайной величины ?, получим.

Пример 3.15. Пусть случайная величина? имеет пуассоновское распределение

вероятностей с параметром X: Тогда ее производящая функция |/(z) есть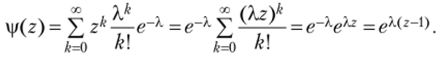

Для характеристик СВ ?, имеем:

Определение 3.29. Характеристической функцией Ф^(7) произвольной действительной СВ ?, называется функция вида.

М) = Ме^, где.

— оо < t < +оо — действительная переменная;  — мнимая единица.

Таким образом, при каждом фиксированном t характеристическая функция совпадает с математическим ожиданием комплексной случайной величины вида r = e'^tS'.

Для целочисленной СВ ?, значение характеристической функции ф,(7) совпадает со значением производящей функции i (t) при z = е", т. е.

Для непрерывно распределенной случайной величины ?, с плотностью распределения вероятностей р (х) характеристическая функция имеет вид.

Дифференцируя ф= (/) но t, получим.

Положив t — 0, получим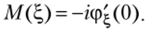

Аналогично может быть получено выражение для дисперсии СВ.

Пример 3.16. Найдем характеристическую функцию СВ Е, ~ Л'(я, о²).

Решение. Найдем вначале характеристическую функцию СВ ?,₀ ~Л'(О, 1):

Так как 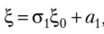, то.

Получили характеристическую функцию случайной величины, распределенной нормально с параметрами а, о².