Разностная аппроксимация дифференциальных уравнений внутрикамерного процесса

Явные схемы Рунге — Кутта второго-четвертого порядка точности

Система дифференциальных уравнений (3.3)—(3.12) с соответствующими замыкающими соотношениями позволяет решать практически все задачи внутренней баллистики многополостных пиромеханизмов в классической постановке без учета перетока пороховых зерен из объема в объем. Будучи дополненными алгоритмами расчета газоприхода в условиях перетока зерен пороха из объема в объем, описанными в предыдущем разделе, эти уравнения позволяют построить модели для описания внутренней баллистики таких многополостных механизмов, в том числе систем разделения реактивных снарядов, в которых отсутствуют протяженные полости с возможным развитием в них нестационарных газодинамических процессов. В рамках реализующего описываемую методику программного комплекса конечно-разностная аппроксимация уравнений (3.3)—(3.12) строится на базе использования явных схем Рунге — Кутта 1—4 порядка точности. Все доступные для использования разностные схемы могут быть представлены в следующей общей форме. На сетке по времени {!",}", = i для системы уравнений.

расчетные формулы задаются соотношениями.

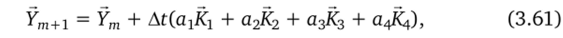
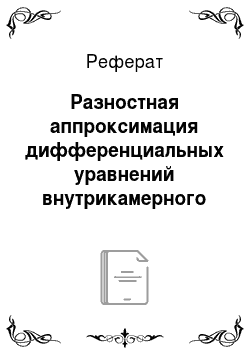
где At = t_m+1 — t_m;

Если N_pK — порядок используемой схемы Рунге — Кутта, задаваемый при расчете, то для.

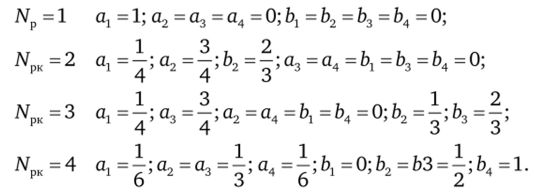
При N_pK = 1 формула (3.61) задает явную схему Эйлера, а при N_pK = = 4 — классическую формулу Рунге — Кутта 4-го порядка точности. Представление расчетных формул в виде (3.61) позволяет удобно размещать промежуточную информацию в памяти компьютера и рассчитывать на каждом шаге по времени столько правых частей К, каков порядок N_pK используемой схемы Рунге — Кутта.

Способы задания шага по времени

Расчет реальных процессов функционироавния пиромеханизмов систем разделения реактивных снарядов и головных частей, описанных в настоящем издании, вряд ли возможен на сетках с постоянным шагом по времени. Это является следствием чередования процессов воспламенения импульсных вышибных зарядов в полостях и процессов последующего расширения или сжатия рабочих тел, которые могут иметь весьма различные временные масштабы. При этом необходимо использовать сетки с переменным шагом по времени, причем величина шага должна выбираться по задаваемой точности расчета автоматически в зависимости от развития внутрибаллистического процесса.

В отдельных случаях, например, при решении модельных задач, когда особенности рассчитываемого процесса легко прогнозируются, может использоваться простейший способ — задание сетки по времени в виде таблицы шагов переменного размера, меняющегося при заданных номерах шагов.

В качестве автоматизированных способов, обеспечивающих адаптацию сетки по времени к особенностям развития вычислительного процесса, реализовано два способа [14] — способ, основанный на использовании метода Рунге, и способ, основанный на вычислении «контрольного члена», задающего главный член локальной погрешности интегрирования.

При использовании метода Рунге оценка локальной погрешности на шаге интеграрования может быть представлена следующим образом.

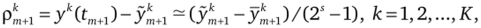
где К — число переменных в решаемой системе дифференциальных уравнений (СДУ); Ут+i — решение СДУ в момент t_m+1, полученное из решения в момент t_m в результате расчета двух шагов по времени разме;

_AtU)₊i j

ром —-— = -(t_m+1 — — решение СДУ в момент f_m+1, получен;

2 2.

ное из решения в момент t_m в результате расчета одного шага по времени размером At^+i = t_m+1 — t_m.

Проверяется допустимость полученной погрешности решения. При этом, если при некотором к

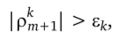
где е*. — наперед заданное значение абсолютной погрешности пременной с номером к, то рассчитанные значения у,"₊₁ иу?₊₁ исключаются из рассмотрения. Выбирается новое значение шага.

и процесс расчета повторяется, пока оценка локальной погрешности не будет удовлетворять условию.

Если оценка локальной погрешности на шаге AtnV+i = t_m+i ^- удовлетворяет неравенствам.

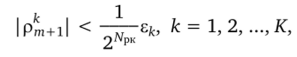
то считается, что достигнута точность расчета, превышающая заданную, и шаг интегрирования удваивается. То есть полагается, что.

и расчет продолжается с шагом At_m+2 от решения у^₊₁, к = 1,2,…, К. Если выполняется неравенство.

то считается, что полученное в точке t_m+1 решение удовлетворяет заданной точности и шаг интегрирования оставляется без изменения.

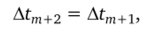
а расчет продолжается от решения y?+i, fc = 1, 2,…, К.

Отметим, что при расчете ГЖТМС, включающих большое количество типовых сосудов, число переменных интегрирования К достаточно велико. При этом нецелесообразно задавать большое число допустимых абсолютных погрешностей параметров е_к. Удобнее задать допустимое значение относительной погрешности 8 одно для всех переменных, а абсолютные погрешности рассчитывать как.

При этом, однако, в случае, если значение |ут₊₁| достаточно мало, весьма малой окажется и величина е_к. Это может привести к зацикливанию при расчете, так как величина шага At_m+2, определяемого алгоритмом, окажется за пределами числа верных цифр в машинном представлении времени.

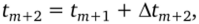
так что t_m+2 и t_m+1 будут восприниматься компьютером как одно число. Аналогично, при очень маленьком шаге по времени приращение решения в формуле (3.61) будет находиться за пределами значащих цифр в машинном представлении числа, и численное решение перестанет изменяться. Такая ситуация возможна, например, при расчете с автоматическим выбором шага процесса с нулевыми начальными условиями. В этом случае расчеты компьютером проводятся, а изменения параметров, включая расчетное время t, не наблюдается.

Для исключения этого явления при малых значениях е_к следует пользоваться задаваемым заранее допустимым значением е_к абсолютной погрешности решения. Окончательно в качестве г_к используется.

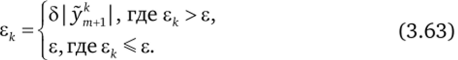
Описанный способ выбора шага удобен тем, что может применяться для всех схем Рунге — Кутта. Однако он весьма неэкономичен, так как требует троекратного решения исходной СДУ даже в тех точках по времени, в которых деления шага пополам не делается. Кроме того он весьма груб, так как критерий выбора мрмента деления или удвоения шага основан на использовании неравенства (3.62), в котором при N_pK = 4 левая граница в 32 раза меньше правой. Поэтому реальный алгоритм расчета строится так, чтобы проверка необходимости смены шага интегрирования делалась не на каждом шаге по времени, а через заданное число шагов, просчитываемое с постоянным шагом, например 3, 5, 10 и т. п. При этом, однако, возможна потеря точности, если начавшийся развиваться в системе импульсный процесс начинается вблизи начала такого интервала.

Более удобным и гибким способом изменения шага по времени в зависимости от развития процесса является использование оценки локальной погрешности шага интегрирования, основанной на комбинации двух специально выбранных формул Рунге — Кутта [194]. Пусть даны две формулы Рунге — Кутта разных порядков точности р и s

i-1.

где К_г =/(t₀, y₀); ^Ki = /(to + «.At, y₀ + At? Pi/KjAt);

;=i.

i-l.

где Kj =f (t₀, y₀y, К₍ =f (t₀ + a. iAt, y₀ + At’ZfiijKjAt), причем p > s, r>r.

i= i.

Будем полагать, что коэффициенты формул (3.64)—(3.65) таковы, что 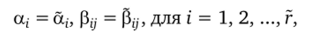то есть и ЯГ, = К, для i = 1, 2,…, г.

Тогда для локальной погрешности менее точной формулы (3.65) получается выражение вида.

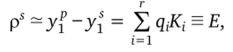
где q, = Р, -Pi для i = 1, 2,…, г и q, = Р; для i = r+ 1,…, г.

Величина Е называется «контрольным членом». Использование контрольного члена при оценке локальной погрешности позволяет выбрать новый шаг по времени вычисляя дополнительно только величины К, для i = г + 1,…, гв более точной формуле (3.64). Таким образом, данный способ существенно более экономичен, чем способ, основанный на методе Рунге.

В рамках рассматриваемой методики реализован следующий алгоритм выбора шага по времени. Наряду с классической схемой Рунге — Кутта четвертого порядка точности (р = 4) рассматривается формула Рунге — Кутта второго порядка точности (5 = 2).

где Щ — те же, что и в (3.63). Контрольный член для формул (3.63) и (3.66) носит название контрольного члена Егорова и имеет вид.

Отметим, что для любой схемы Рунге — Кутта главный член локальной погрешности метода с точностью до 0(ДР'⁺¹) представляется в виде.

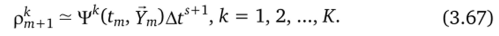
Принимая в качестве оценки р"+ величину контрольного члена Егорова Е^к и задавая допустимую абсолютную погрешность вц, переменной у^к, проверяем условие

Если оно выполняется, то полагаем, что при данном шаге Atm+i метод не достигает требуемой точности и следует уменьшить шаг по времени, выбрав.

где, а определяется из условия выполнения равенства 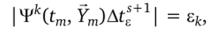или, подставляя в (3.67) контрольный член Е^к,

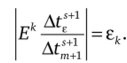
Отсюда.

Если вместо (3.68) выполняется обратное неравенство.

то из формулы (3.69) получаем, а > 1, At_s > At_m+1.

Таким образом строится гибкий алгоритм выбора шага по времени, причем шаг по времени корректируется на каждом шаге расчета домножением на множитель, а > 1 или, а < 1.

На практике, применительно к контрольному члену Егорова, а рассчитывается по формуле.

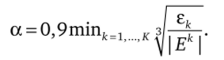
Коэффициент 0,9 берется для того, чтобы в случае увеличения шага At (а > 1), уменьшить вероятность необходимости его уменьшения на следующем шаге. Расчет, а ведется на каждом шаге по времени. При этом СДУ решается с использованием формулы Рунге — Кутта четвертого порядка точности. При получении, а < 1 рассчитанное значение Y_{m +} i отбрасывается и рассчитывается вновь с шагом At_e > aAt_m+1. В качестве с_к выбираются величины, задаваемые в соответствии с (3.63).