Интервальные оценки параметров случайной величины

Пусть по результатам опыта построена точечная оценка, а параметра а₀. Точечная оценка, а параметра а₀ дает лишь некоторое приближенное значение а₀.

Возникает вопрос: насколько эта оценка точна и достоверна? Чтобы получить представление о точности и надежности оценки, используют интервальную оценку параметра.

Интервальная оценка параметра а₀ (лг₀ или а^) признаках генеральной совокупности имеет следующий вид:

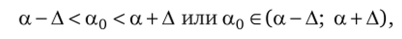
где Д — наибольшее отклонение выборочного значения параметра от его истинного значения, или предельная ошибка выборки (точность оценки, отклонение).

Очевидно, что это неравенство (или попадание а₀ в указанный интервал) при заданной точности оценки Д верно лишь с какой-то вероятностью у, которая называется доверительной вероятностью. На практике обычно заранее задают доверительную вероятность у, причем наиболее часто берут значения у = 0,95, у = 0,99 и у = 0,999.

Интервал (а — Д; а + Д) называется доверительным интервалом. В качестве а берут точечную несмещенную оценку а₀, полученную по результатам выборки. Следовательно, задача состоит в том, чтобы по заданной величине у найти Д.

Такимобразом, чтобы получить интервальную оценку генеральной средней х₀, нужно найти такую величину А, для которой.

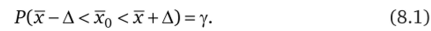
Пусть известна генеральная дисперсия ст§ признака X. Так как неравенство х-Д<�х₀ эквивалентно неравенству лг<�лг₀+Д, а неравенство х₀ < х + А эквивалентно неравенству х₀ — А < х, то выражение (8.1) эквивалентно выражению.

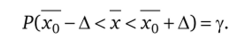
Здесь х— случайная величина, и если признак X распределен нормально,_то х тоже распределена нормально. Так как х — несмещенная оценка х₀, то Мх — х₀.

Можно доказать, что если дисперсия признака X равна о%, то дисперсия случайной величины х, являющейся средним арифметическим п одинаково распределенных случайных величин с дисперсией ст§,.

.

равна —-, а среднее квадратическое отклонение случайной величины.

п

Сто.

х, следовательно, равно —?=.

1п

Тогда можно также показать, что 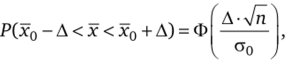где §(х) — функция Лапласа.

Отсюда следует, что для нахождения, А нужно решить уравнение.

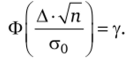
Уравнение решается так. Обозначим t = ^ ^ и найдем по таблице значений функции Лапласа Ф (0 (приложение 3) такое t, чтобы Ф (Г) было равно у.

Вычислим окончательно, А по формуле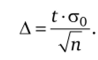

Следовательно, доверительный интервал х₀ для доверительной вероятности у имеет вид.

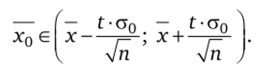
Такую оценку используют, когда объем выборки п > 30.

Если генеральная дисперсия неизвестна, то часто ее заменяют ее несмещенной оценкой s², хотя при небольших п это ведет к существенному уменьшению доверительного интервала.

Доверительный интервал получается точнее, если при этом вместо t взять параметр t_y распределения Стьюдента, который можно найти по таблице (см. приложение 5) по известным значениям у и п.

Тогда доверительный интервал для генеральной средней при неизвестной генеральной дисперсии имеет вид.

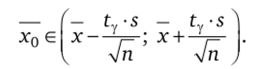
Замечание. Если нет дополнительных ограничений, параметр Стьюдента при объеме выборки рекомендуется применять, когда он не превышает 30.

Пример 8.2.

Эксперт произвел выборку из большой партии электроламп для выявления брака, в выборке оказалось 100 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000 ч.

Найти с доверительной вероятностью у = 0,95 доверительный интервал для средней продолжительности горения лампы применительно ко всей партии, если известно, что случайная величина, равная продолжительности горения лампы, распределена нормально, а дисперсия этой случайной величины равна 1600 ч².

Решение. Обозначим X — продолжительность горения случайно взятой лампы из партии. Тогда по условию задачи п =100; х = 1000; DX = = 1600,.

а ст₀ = 40.

По таблице функции Лапласа (приложение 3) находим t = 1,96 как решение уравнения Ф (г) = 0,95. Тогда точность интервальной оценки Д равна.

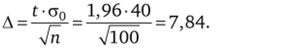
Следовательно, доверительный интервал имеет вид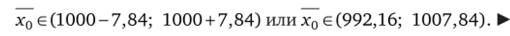

Пример 8.3.

Найти с доверительной вероятностью у = 0,99 доверительный интервал среднего роста заключенных следственного изолятора по данным более раннего примера в предположении, что рост заключенных распределен нормально.

Решение. Обозначим X — рост случайно выбранного заключенного. Тогда по условию задачи и произведенным вычислениям п = 100, х = 166, s = 5,81.

Так как генеральная дисперсия неизвестна, то по таблице значений критерия Стьюдента (приложение 5) по значениям п = 100 и у = 0,99 находим t" = = 2,63.

Тогда точность интервальной оценки Д равна.

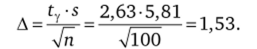
Следовательно, доверительный интервал имеет вид.

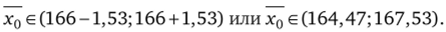
Можно показать, что вычисления интервальной оценки с помощью функции Лапласа дает практически такой же результат. Это объясняется достаточно большим объемом выборки. ?