Составные структуры. 
Информатика и математика

В результате освоения данной темы студент должен: знать

• • основные понятия теории графов;
• • алгоритмы решения типовых задач; уметь
• • проводить расчеты с использованием графов;
• • строить схемы решения задач; владеть
• • методикой проведения расчетов при решении специальных задач юриспруденции;
• • навыками анализа и реферирования научной литературы по данной теме.

Основные понятия теории графов

Существует ряд задач, которые удобно представлять в виде графических структур. Например, графически можно формализовать процесс принятия решения, функционирование производственной системы, транспортировку продукции, передачу информации и т. д.

Анализ графических структур позволяет находить оптимальные (наилучшие) решения этих задач. Для построения и исследования графических структур разработана система методов, изучаемая в теории графов. Основным объектом этой теории является граф.

Граф можно определить как некоторое множество точек плоскости и множество отрезков прямых или кривых линий, соединяющих все или некоторые из этих точек.

Эти точки символизируют объекты какой угодно природы (люди, города, учреждения и т. д.), а соединяющие их линии изображают связи между ними (наличие дорог между городами, чувства или деловые отношения между людьми и т. д.).

Таким образом, граф G представляет собой совокупность двух множеств X = {х_1; х₂,…, х"} и U = {Uy}, i, j =1,…, пи обозначается G= (X, U).

Элементы множества X называются вершинами графа и изображаются точками плоскости. Элементы множества U изображаются отрезками прямых или кривых линий, соединяющих некоторые вершины. Взаимное расположение, форма и длина упомянутых отрезков значения не имеют. Важно лишь, что они соединяют две данные вершины.

Пример графа представлен на рис. 4.1.

Если в паре вершин (х,-, хЛ указано направление связи, т. е. определено, какая из них является первой вершиной, то соединяющий их направленный отрезок и,-, называется дугой. При этом и^ u_;i.

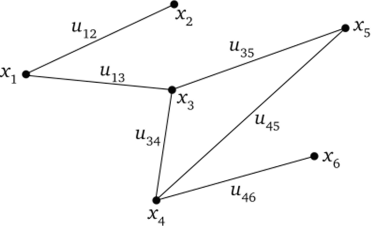
Рис. 4.1. Расположение ребер в графе

Если же ориентация не указана, то отрезок называется ребром, a Uy = Uj_t. Вершины х_; и Xj, определяющие дугу (ребро) и^, называются ее (его) концевыми вершинами.

Вершины в графе называют смежными, если они различны и существует дута (ребро), соединяющая эти вершины. Если две дуги (ребра) имеют общую концевую вершину, они также называются смежными.

Если обе концевые вершины дуги (ребра) совпадают, то дугу (ребро) и" называют петлей (рис. 4.2, а). На графе могут существовать дуги (ребра) с одинаковыми концевыми вершинами.

Будем называть такие дуги (ребра) параллельными (рис. 4.2, б, в). Говорят, что дуга (ребро) инцидентна своим концевым вершинам, и обратно — вершины инцидентны своей дуге (ребру).

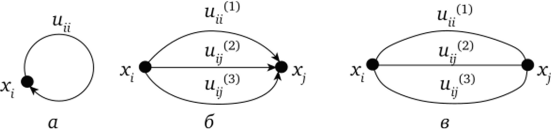
Рис. 4.2. Виды дуг (ребер):

а — петля; б — параллельные дуги; в — параллельные ребра Граф называют простым, если он не содержит петель и параллельных дуг (ребер). Простой граф, в котором каждая пара вершин смежная, называется полным. Граф, содержащий хотя бы две параллельные дуги (ребра), называется мулътиграфом.

Если в графе G все элементы множества U — дуги, то граф называется ориентированным или орграфом (рис. 4.3, а). Если в графе G все элементы множества U — ребра, то граф называется неориентированным (рис. 4.3, б).

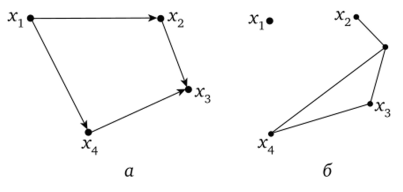
Рис. 4.3. Виды графов:

а — орграф; б — неориентированный граф Поскольку при изображении графа его вершины можно располагать произвольно и по своему усмотрению выбирать форму соединяющих их линий, то один и тот же граф можно представить в различных видах. О таких графах говорят, что они изоморфны.

То есть два графа G и G' изоморфны (рис. 4.4), если между множествами их вершин существует такое взаимно однозначное соответствие, при котором в одном из графов отрезками соединены вершины в том и только в том случае, если и в другом графе отрезками соединены соответствующие вершины (при этом нумерация вершин может быть различной). В орграфах следует также учитывать ориентацию.

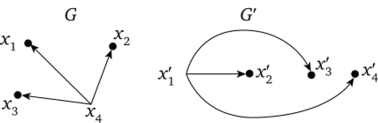
Рис. 4.4. Изоморфные ориентированные графы G и G'

На рис. 4.4 вершина х_г соответствует вершине х'₂; вершина х₂ — вершине х'₄; вершина х₃ — вершине х₃; вершина х₄ — вершине х{.

Вершины в графе могут отличаться друг от друга количеством дуг (ребер), которым они инцидентны.

Степенью Р (х_;) вершины х_; называется число дуг (ребер) графа G, инцидентных данной вершине. Так, на рис. 4.5 степень вершины х₂ равна 1, т. е. Р (х₂) = 1, Р (х₃) = 3, Р (х₄) = Р (х₅) = 2.

Вершина степени 0 называется изолированной. То есть вершина X] на рис. 4.5 изолированная.

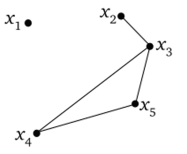
Рис. 4.5. Степени вершин

Для орграфа вводятся понятия полустепени захода Р⁺ (х,) вершины х, — — это количество дуг, входящих в х" и полустепени исхода Р~(х,) — это количество дуг, исходящих из х,. Понятно, что.

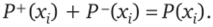
Например, на рис. 4.6 полустепени вершин: Р+СхД = 1; Р~(х_г) = 2; Р+(х₃) = 1; Р"(х₃) = 2 и т. д.

Путем в орграфе называется любая последовательность дуг, в которой конец каждой предыдущей дуги совпадает с началом следующей. Путь, у которого начальная вершина совпадает с конечной, называется контуром (рис. 4.7).

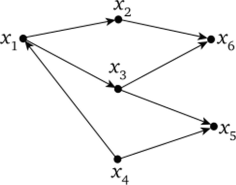
Рис. 4.6. Полустепени вершин

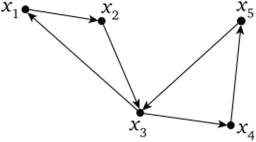
Рис. 4.7. Пути графа:

• *i *2*з — путь;
• *1*2 *3*1 — контур

В неориентированном графе последовательность ребер, в которой каждые два соседних ребра смежные, называется маршрутом.

Маршрут, в котором все ребра различны, называется цепью. Замкнутая цепь именуется циклом (рис. 4.8).

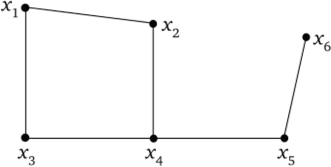
Рис. 4.8. Маршруты графа:

х₂ х₄ Х5 — цепь; х, x₂x₄x₃Xf — цикл Важным понятием в теории графов является связность. Неориентированный граф называется связным, если любые две его вершины можно соединить маршрутом, а в противном случае — несвязным.

Неориентированный связный граф без циклов называется деревом.

У графа, который является деревом, число ребер на единицу меньше числа вершин. Как показано на рис. 4.9, а, дерево не содержит циклов, любые две его вершины можно соединить единственной цепью.

Для графов, которые сами по себе не являются деревьями, вводится понятие остовного дерева.

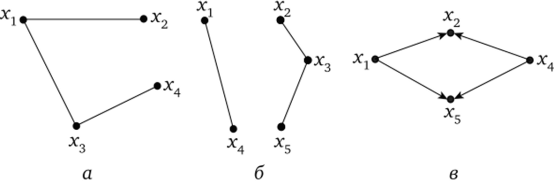
Рис. 4.9. Примеры связных и несвязных графов:

а — связный неориентированный граф без циклов (дерево); б — несвязный неориентированный граф; в — не сильно связный орграф.

Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Пусть G — связный граф. Тогда остовное дерево графа G (если оно существует) должно содержать (п 3- 1) ребер.

Для установления связности орграфа ориентацию его дуг принимать в расчет не следует. Для орграфа существует еще понятие сильной связности. Говорят, что орграф сильно связный, если между любыми двумя его вершинами существует хотя бы один путь (см. рис. 4.9).

Связный неориентированный граф G называется эйлеровым, если в нем существует замкнутая цепь (цикл), проходящая через каждое его ребро (естественно, по одному разу, так как это цепь).

Такой цикл также называется эйлеровым циклом (рис. 4.10, а). Если в графе существует замкнутый цикл, проходящий через каждую вершину графа по одному разу (кроме, естественно, начальной — конечной вершины), то такой цикл называется гамильтоновым и сам граф также называется гамильтоновым (рис. 4.10).

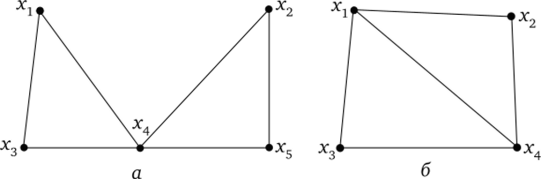
Рис. 4.10. Примеры эйлерова и гамильтонова графов:

а — эйлеров граф (эйлеров цикл: б — гамильтонов граф.

(гамильтонов цикл: х₁х₂х₄х₃х₁)

В полном графе всегда существуют гамильтоновы циклы. Частные случаи наличия циклов в графах приведены на рис. 4.11.

В различных приложениях теории графов, моделирующих реальные процессы, дугам (ребрам) обычно сопоставляют какие-либо числовые характеристики (расстояние между городами, величина денежных выплат и т. д.).

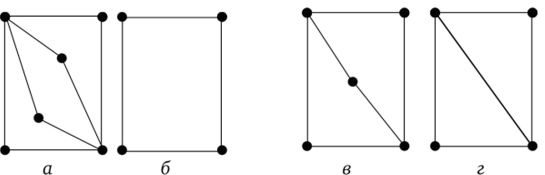
Рис. 4.11. Частные случаи наличия циклов в графах:

а — в графе есть эйлеров цикл, но нет гамильтонова цикла; б — в графе есть и эйлеровый и гамильтонов циклы; в — в графе нет ни эйлерова, ни гамильтонова цикла; г — в графе есть гамильтонов, но нет эйлерова цикла В подобных случаях говорят, что дугам (ребрам) графа приписаны определенные веса, а граф G с весами на дугах (ребрах) называют взвешенным.

Сумма весов всех дуг (ребер) называется весом графа.

Пример взвешенного графа показан на рис. 4.12.

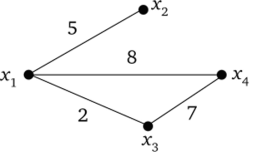
Рис. 4.12. Взвешенный граф