Основные этапы работы

• 1. Задача исследования формализуется в виде статистической гипотезы, т. е. выбираются те статистические характеристики, которые будут подвергнуты проверке (средние, доли, коэффициенты и др.).
• 2. Выдвигается #₀ (испытуемая) и Н_] (альтернативная, конкурирующая) гипотезы.
• 3. Определяется ошибка, а (I рода), чаще всего от 1 до 10%, а также в зависимости от конкретной задачи и оценки рисков решается вопрос, будет ли проверка односторонней или двусторонней.
• 4. После этого фиксируется критическая точка соответствующего критерия (t, F, х²у Т), делящая всю площадь под нормальной кривой на область принятия #₀ и на критическую область (зону), отклоняющую #₀.
• 5. По специальным формулам рассчитывается фактическое значение критерия и сравнивается с табличным (теоретическим).
• 6. Если фактическое значение критерия меньше табличного, то #₀ отклонить не удается. Обратная ситуация, а именно если фактическое значение критерия попадает в критическую область, то делается вывод об отклонении нуль-гипотезы и принятии альтернативной.

Сравнение средних двух выборок (гг > 30).

Предположим, что в двух случайных выборках работников численностью п_л = 23 и п₂ = 30 средняя выработка за смену составляет Хл = 11,6, 5г₂ = 13 единиц соответственно при дисперсиях af = 4,1 и а₂ = 5,03. Можно ли считать такое расхождение случайным или же оно является следствием различных условий организации труда?

Ошибку I рода, а принимаем на уровне 5%. Нулевая гипотеза Я₀: х_х = х₂; альтернативная Н_х: х_{ ф х₂, т. е. либо х_{ > х₂, либо х_х < х₂ (двусторонняя проверка).

Выписываем формулу критериальной статистики и находим фактическое значение:

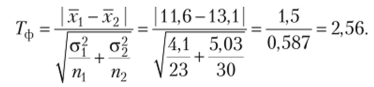
Приняв уровень значимости а = 5%, мы тем самым определили критическую точку, разделяющую область принятия Н₀ от области ее отклонения. По таблице интеграла вероятностей и при доверительной вероятности 1 — 0,05 = 0,95 находим 7'_кр = 1,96. Тф > 7'_кр, т. е. Тф = 2,56 попадает в критическую зону, отклоняя тем самым нулевую гипотезу. Сам факт отклонения гипотезы 7/₀ нс означает, что она является ложной. Напомним, что принятый нами уровень 5%, или 0,05, означает, что в 5 случаях из 100 мы рискуем допустить а, т. е. отвергнуть верную гипотез}' (рис. 8.1 и 8.2).

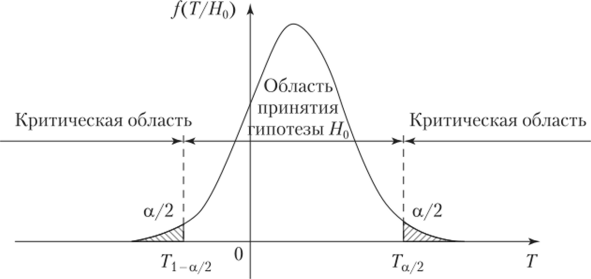
Рис. 8.1. Двусторонняя критическая область при, а = 0,05.

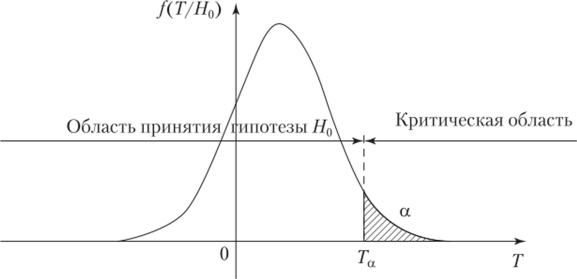
Рис. 8.2. Односторонняя критическая область при, а = 0,05.

Сравнение двух выборочных дисперсий (и < 30).

Предположим, что известны объемы и выборочные исправленные дисперсии двух выборок: п, = 9; s² = 1,4 и п₂ = 12; s² = 4,7. На уровне значимости 0,05 необходимо проверить гипотезу Я₀: а² = а² против конкурирующей гипотезы Я: а² * а|.

Проверяем гипотезу Я": о'² = а| генеральной совокупности.

Рассчитываем фактические значения критерия F Фишера — Снедекора (большая исправленная дисперсия всегда в числителе) и получаем F₍|, = 4,3/1,4 = 3,07. Из таблицы критических точек F-распределения Фишера (см. [401) находим F_Kp = 3,31. При а — 0,05 F_Kp > F₍|,. Вывод: нет основания отклонить гипотезу Н₀ о равенстве дисперсий, различия между дисперсиями несущественные, случайные.

Сравнение двух выборочных долей (%) (и > 30).

Предположим, что проводились клинические испытания нового лекарства. В выборке участвовало 830 мужчин и 945 женщин. У 36 мужчин и 60 женщин наблюдались неблагоприятные побочные явления. Можно ли утверждать, что у женщин побочные явления возникают чаще?

^ноРм = Рж>

Н-Р_Ы*Р_Ж.

Введем обозначения: п_ы = 830; п_ж = 945.

Доля (%) мужчин с побочными явлениями р_ы = 36: 830 = 0,0433 (4,33%); доля (%) женщин, с побочными явлениями р_ж = 65: 945 = = 0,0688 (6,88%). р — средняя доля мужчин и женщин, имеющих побочные явления: р = (36 + 60): 1775 = 0,054; q = 1 — р = 0,946; pq = 0,051. Статистика имеет следующий вид:

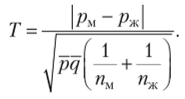
Уровень значимости 0,03 (3%), проверка двусторонняя.

Подставляем в формулу полученные значения и получаем Тф = 2,32. Учитывая выбранный нами уровень значимости 0,03, по таблице интеграла вероятностей находим 1 — 0,03 = 0,97, Т_кр = 2,17.

Вывод: 7ф превышает Г_кр и попадает в критическую зону (правее точки 2,17), тем самым отвергая Н₀: р_и = р_ж. Принимаем конкурирующую Я: р_м *р_ж, т. е. мы вправе сделать вывод, что лекарство действует по-разному на мужчин и женщин, и что различие не является случайным, такой вывод сделан с вероятностью 0,97.

Заметим, кстати, что если бы мы сформулировали //: р_ж> р_м, то вывод был бы тем же самым. При 3%-ном уровне значимости Г_кр при односторонней проверке равно 1,89. Двусторонняя проверка более «строгая», нежели односторонняя. Рубеж 2,17 преодолеть труднее, чем 1,89. Будет ли проведена односторонняя или двусторонняя проверка — решается по смыслу самой задачи, т. е. нас интересует факт различия в обе стороны или только в одну.

Приведем пример ситуации, когда Я₀ нельзя отклонить. По многолетним данным средний проходной балл составлял 50 с дисперсией 151,3. Многие эксперты считали, что величина балла несколько занижена (что ведет к набору слабо подготовленных школьников), и предлагали поднять планку до 54. Для проверки этого предположения была произведена случайная выборка п — 30 школьников, которые набрали х_в = 54. Необходимо проверить, существенно ли различие х_г = 50 и х_в = 54 при уровне значимости а = 0,02 (2%), правосторонняя проверка; Я₀: х_в = х_г; Яр х_в > х_г.

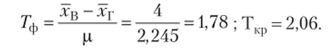
Вывод: //₍₎ отклонить не удалось. Проходной балл остается х = 50. А что если на самом деле верна Яр х_г = 54, т. е. школьники теперь лучше подготовлены? Если это так, то, принимая Я₀, мы допускаем ошибку II рода р (вероятность принять неверную гипотезу). Ошибку Р и мощность критерия М = 1 — Р можно посчитать по-разному. В нашем случае М = 0,5 — Ф (2,06 — 1,78) = 0,5 — - Ф (0,28) = 0,39; Р = 0,61. Это вероятность того, что не будет ошибочно принята ложная гипотеза Я₀: х = 50.

При одновременном фиксировании, а и Р до проведения выборочного исследования необходимо определить требуемый объем выборки, что может быть сделано применительно к нашим условиям (а = 0,02; Р = 0,61; п = 30). Если бы мы приняли, а = 0,02, Р = 0,1, то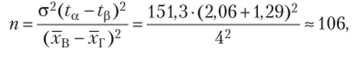

т.е. объем выборки следовало бы увеличить в 3,5 раза.

Сравнение средних двух независимых малых выборок (и < 30).

Сравнение двух средних генеральных совокупностей при условии, что выборки независимы и невелики по объему, а дисперсии генеральной совокупности неизвестны, но одинаковы, проводится в следующем порядке.

Сначала извлекаются две малых выборки п_х и п₂. По этим выборкам рассчитывают х, и х₂, а также исправленные выборочные дисперсии, обозначаемые в данном случае как 5[ и 5|. Затем выдвигается Я₀: х, = х₂ и альтернативная гипотеза //: х, Ф х₂. Уровень значимости принимается, как обычно, от 0,01 до 0,10, чаще всего 0,05.

В качестве критерия принимается случайная величина.

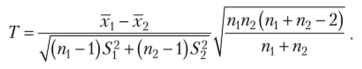
Доказано, что величина Т при справедливости Я₀ имеет ?-распределение Стьюдента с числом степеней свободы п_л + п₂- 2.

Рассмотрим пример. Произведены две независимые выборки П — 6 и п₂ = 9; по ним получены х_х = 2,8 и х₂ = 3,5; S_x = 0,33 и 5| = 0,33. По условию заданные выборочные исправленные дисперсии не равны друг другу. Поэтому сначала по критерию Фишера необходимо проверить гипотезу о равенстве генеральных дисперсий.

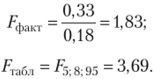
Так как Тф_акт < Т_хаб_л> нулевая гипотеза о равенстве генеральных дисперсий не может быть отклонена.

Далее, подставляя конкретные значения в формулу, имеем.

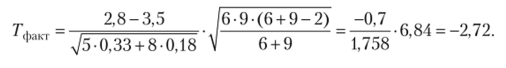
По таблице распределения Стьюдента находим t_005;13= 2,16. Т-гибл ⁼ 2,72 > 2,16. Следовательно, гипотезу о равенстве генеральных средних отвергаем. Различие существенно.

Сравнение средних двух малых зависимых выборок (и < 30).

Часто необходимо проверить гипотезу о равенстве двух средних генеральных совокупностей при условии, что выборки зависимы. Имеется в виду, что изучение одной и той же выборки производится дважды: до и после некоторого события, например самочувствие больных до и после приема лекарства, знания студентов до и после дополнительных занятий с ними, результаты анализа двух лабораторий, количество продаж товаров до и после рекламной акции и т. п.

Для решения подобных задач необходимо вычислить значение критерия.

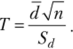
Сформулируем нулевую и альтернативную гипотезы: Н₀: х_х -х₂; Я,: х, > х₂; а = 0,05; ?_крит распределения Стьюдента = 1₀₉₅.₉ = 1,83. Приведем иллюстрирующий пример.

Пример 8.5.

При подготовке к олимпиаде, но математике было отобрано 10 студентов. Результаты решения задач до и после проведения дополнительных занятий (в баллах) приведены в табл. 8.6; d — разность в баллах, сР — их квадраты.

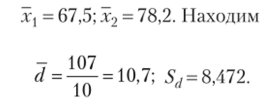
Таблица 8.6.

Данные примера для проверки гипотез о равенстве средних двух генеральных совокупностей.

Подставляя в формулу полученные значения, находим.

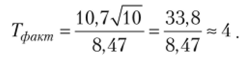
7ф_акт > Г_табл, которое рассчитывается по распределению Стьюдента Я,: х₂ > Х — <�о, 9 г,; 9 ⁼ 1 >83. Поскольку 7ф_акт значительно больше |<| =1,83, делаем вывод, что расхождение между средними значимо и дополнительные занятия сыграли положительную роль.

Сравнение двух выборочных коэффициентов вариации (п >30).

В ряде случаев при проверке статистической гипотезы о равенстве средних в генеральной совокупности нулевую гипотезу не удается отклонить, г. е. на основании эксперимента (опыта) приходим к выводу, что Х = х₂- Это важная информация, но ее возможно следовало бы дополнить показателем разброса (колебания). Действительно, равенство двух (и более) средних величин недостаточно для суждения об однородности (гомогенности) совокупности. Так, например, равенство средних баллов в двух группах ничего нам не сообщает о вариации внутри групп. Одна группа (футбольная команда, сорт зерновых и т. п.) стабильна, устойчива, с небольшим разбросом, другая, наоборот, состоит из 3—5 отличников и 7—8 двоечников при одинаковых средних. Для выяснения этих различий хорошо подходят коэффициенты вариации, сравнение которых позволяет получить ответ на вопрос об однородности двух выборок. Приведем пример.

Имеются две группы — выборки п_{ = 29 и п₂ = 36. = 33%;

K_G2 = 47%. #₀: К_а| = K_Gi) при Н_х: /С_а| Ф K_G2. Проверка осуществляется обычным образом, критерий имеет следующий вид:

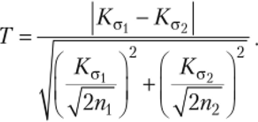
Напоминаем, что К_а/^2п — это приближенная оценка среднеквадратической ошибки коэффициента вариации. Подставляя полученные значения в формулу, имеем:

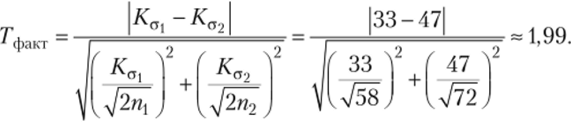
При, а = 0,05 Г_табл = 1,96, Гф_акт (1,99) > Г_табл (1,96). Полученное значение Гф_акт * Г_табл свидетельствует о трудности сделать однозначный вывод касательно однородности обеих выборок. Было бы желательно увеличить объемы выборок и повторить сравнение. О правильности такого решения говорит и величина показателя точности опыта Р, превышающая 5%.

Показатель точности опыта выражает ошибку средней арифметической и, таким образом, служит показателем точности определения последней.