ЗАДАНИЕ 3-б. РАСЧЕТ БАЛОК НА ПРОЧНОСТЬ ПРИ ПЛОСКОМ ИЗГИБЕ

Пример выполнения задания. Дано: схема балки (рис. 15);

На изгиб работают балки, валы, оси и другие детали различных конструкций. В качестве примера можно привести межэтажные перекрытия зданий и сооружений, консольные балки балконов и козырьков, мостовые балки и т. п. В данной работе рассмотрен изгиб брусьев, имеющих хотя бы одну плоскость симметрии, а плоскость действия нагрузок совпадает с ней.

При поперечном изгибе в любом поперечном сечении возникают деформации растяжения и сжатия, сдвига. Основой расчета на прочность большинства балок является расчет по нормальным напряжениям. В отличие от деформаций при центральном растяжении и сжатии напряжения, возникающие при поперечном изгибе, неравномерно распределяются по площади поперечного сечения и зависят не только от его площади, но и от формы сечения. Поэтому для экономически обоснованного расчета необходимо выбрать рациональные размеры и форму сечения.

1. Определение реакций опор балки от заданной нагрузки.

Покажем внешние силы, приложенные к балке: пара сил с моментом М; силу Р1, распределенную нагрузку интенсивностью q и реакцию опоры, А (рис. 15).

Реакция в опоре, А (консольная заделка) раскладывается на две составляющие — ZA и YA и момент МA.

Составим уравнения равновесия сил, приложенных к балке:

Из этих уравнений ZА = 0 кН; YA = 43 кН; МA = 171,6 кН•м.

Для проверки правильности вычислений составим уравнение моментов сил относительно точки B:

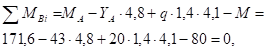
то есть реакции опор найдены верно.

Расчетная схема балки приведена на рис. 16.

2. Построение эпюр поперечных сил Q и изгибающих моментов .

Разбиваем балку на участки. За границы участков принимаются сечения, в которых приложены сосредоточенные силы, моменты и начинает или заканчивает действие распределенная нагрузка. Рассматриваемая балка делится на три участка.

Запишем уравнения для определения внутренних силовых факторов для каждого из участков.

I участок ():

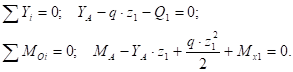
Рис. 17. Участок I

Отсюда.

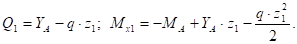
На границах участка:

при м кН•м;

при.

II участок ():

Рис. 18. Участок II

Отсюда На границах участка:

при.

при.

III участок ():

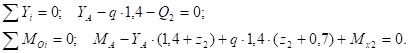
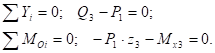
Рис. 19. Участок III

Отсюда На границах участка:

при м.

при.

По полученным значениям строим эпюры поперечных сил и изгибающих моментов (рис. 16).

3. Определение положения опасного сечения.

Опасное сечение расположено в том месте, где модуль изгибающего момента имеет максимальное значение.

В рассмотренном примере оно расположено на границе первого участка, где.

4. Определение расчетного осевого момента сопротивления сечения.

Из условия прочности по нормальным напряжениям.

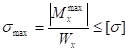
находим расчетный осевой момент сопротивления сечения балки с учетом того, что [?] = 140 МПа:

Определение размеров наиболее распространенных сечений балок.

Кольцо с соотношением? = d/D = 0,75:

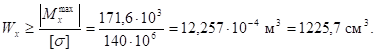
Квадрат:

Швеллер: по таблице сортамента прокатной стали (ГОСТ 8240) подбираем швеллер с моментом сопротивления большим или равным расчетному. В данном случае такого швеллера нет, поэтому в расчет его не включаем.

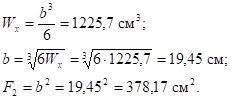
Сравнение масс полученных балок.

Для выбора наиболее экономичного варианта изготовления сравним массы балок различного поперечного сечения. При прочих равных условиях массы балок относятся так же, как и площади их поперечных сечений:

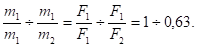
Таким образом, наиболее выгодной является балка кольцевого сечения, масса которой, а, следовательно, и стоимость, в 1,58 раза меньше, чем у балки квадратного сечения.