Изображение графов на плоскости

При изображении графов на рисунках чаще всего используется следующая система обозначений: вершины графа изображаются точками или, при конкретизации смысла вершины, прямоугольниками, овалами и др. где внутри фигуры раскрывается смысл вершины (графы блок-схем алгоритмов). Если между вершинами существует ребро, то соответствующие точки (фигуры) соединяются отрезком или дугой. В случае ориентированного графа дуги заменяют стрелками, или явно указывают направленность ребра. Различают планарные и непланарные графы. Планарный граф — это граф, который можно изобразить на рисунке без пересечения рёбер (простейшие — треугольник или пара связанных вершин), иначе — непланарный. В том случае, если граф не содержит циклов (путей однократного обхода рёбер и вершин с возвратом в исходную вершину), его принято называть «деревом». Важные виды деревьев в теории графов — бинарные деревья, где каждая вершина имеет одно входящее ребро и ровно два выходящих, или является конечной — не имеющей выходящих рёбер.

Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет (другими словами, изоморфны ли соответствующие изображениям графы). В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

Виды раскрасок

Раскраска вершин Когда говорят о раскраске графов, почти всегда подразумевают под этим раскраску их вершин, то есть присвоение цветовых меток вершинам графа так, чтобы любые две вершины, имеющие общее ребро, имели разные цвета. Так как графы, в которых есть петли, не могут быть раскрашены таким образом, они не являются предметом обсуждения.

Терминология, в которой метки называются цветами, происходит от раскраски политических карт. Такие метки как красный или синий используются только когда число цветов мало, обычно же подразумевается, что метки являются целыми числами .

Раскраска с использованием цветов называется -раскраской. Наименьшее число цветов, необходимое для раскраски графа называется его хроматическим числом и часто записывается как. Иногда используется, с тех пор как обозначает Эйлерову характеристику. Подмножество вершин, выделенных одним цветом, называется цветовым классом, каждый такой класс формирует независимый набор. Таким образом, -раскраска — это то же самое, что и разделение вершин на независимых наборов. граф хроматический многочлен вершина Хроматический многочлен.

Хроматический многочлен — это функция, которая считает число t-раскрасок. Из названия следует, что для заданных эта функция — полином, зависящий от t. Этот факт был обнаружен Биркгофом и Льюисом при попытке доказать гипотезу четырёх красок.

Все не изоморфные графы из 3 вершин и их хроматические многочлены. Пустой граф E3 (красный) допускает раскраску одним цветом, остальные — нет. Зелёный граф может быть раскрашен 3 цветами 12 способами.

Например, граф на изображении справа может может быть раскрашен 12 способами с использованием 3 цветов. Двумя цветами он не может быть окрашен в принципе. Используя 4 цвета, мы получаем 24+4*12 = 72 вариантов раскраски: при использовании всех 4 цветов, есть 4! = 24 корректных способа (каждое присвоение 4 цветов для любого графа из 4 вершин является корректным); и для каждых 3 цветов из этих 4 есть 12 способов раскраски. Тогда, для графа в примере, таблица чисел корректных раскрасок будет начинаться так:

Для графа в примере,, и конечно, .

Хроматический многочлен содержит по меньшей мере столько же информации о раскрашиваемости, сколько и хроматическое число. В самом деле, — наименьшее целое положительное число, не являющееся корнем хроматического многочлена.

Реберная раскраска.

Реберная раскраска графа подразумевает под собой назначение цветов ребрам так, что никакие два ребра одного цвета не принадлежат одной вершине. Эта задача эквивалентна разделению множества граней на множества независимых граней. Наименьшее число цветов, необходимое для реберной раскраски графа — это его хроматический индекс, или реберное хроматическое число,. Например, рис. 5 показывает рёберную раскраску графа в красный, синий и зелёный цвета. Рёберная раскраска — это один из видов различных типов раскраски графов. Задача рёберной раскраски задаётся вопросом, можно ли раскрасить рёбра заданного графа максимум в различных цветов для заданного значения или для минимального возможного числа цветов. Минимальное требуемое число цветов для раскраски рёбер заданного графа называется хроматическим индексом графа. Например, рёбра графа на иллюстрации можно раскрасить в три цвета, но нельзя раскрасить в два, так что граф имеет хроматический индекс три.

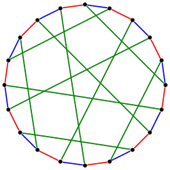
По теореме Визинга, число цветов, необходимых для рёберной раскраски простого графа либо равно максимальной степени, либо. Для некоторых графов, таких как двудольные графы и планарные графы высокой степени, число цветов всегда равно, а для мультиграфов число цветов может быть вплоть до. Существуют алгоритмы полиномиального времени, создающие оптимальную раскраску двудольных графов и раскраску простого не двудольного графа с числом цветов. Однако, в общем случае, задача поиска оптимальной рёберной раскраски NP-полна и самый быстрый из известных алгоритмов для неё работает за экспоненциальное время. Изучались много вариантов задачи рёберной раскраски, в которых условия назначения цвета ребру должны удовлетворять другим условиям, а не сопряжённости.

Тотальная раскраска.

Тотальная раскраска — это один из видов раскраски вершин и ребер графа. Под ней подразумевают такое присвоение цветов, что ни соседние вершины, ни смежные ребра, ни вершины и ребра, которые их соединяют, не имеют одинакового цвета. Полное хроматическое число графа — это наименьшее число цветов, необходимое для любой полной раскраски.

Свойства

Свойства хроматического многочлена.

• · Если — пустой граф,
• · Если граф — объединение непересекающихся подграфов и ,
• · Если в есть петля,

Ограничения на хроматическое число.

• · Назначение всем вершинам разных цветов всегда дает правильную раскраску, так что
• · Единственный вид графов, которые могут быть раскрашены одним цветом — это нулевые графы.
• · Полный граф, состоящий из вершин требует цветов.
• · При оптимальной раскраске должно быть по меньшей мере одно ребро из ребер графа между каждыми двумя цветовыми классами, так что
• · Если является объединением непересекающихся подграфов и, то
• · Если содержит клики размера k, тогда необходимо минимум k цветов для раскраски этой клики, другими словами хроматическое число больше, либо равно размерности клики:

Для интервальных графов это ограничение точно.

• · По теореме 4 цветов, любой плоский граф может быть раскрашен 4 цветами.
• · 2-раскрашиваемые графы — это двудольные графы, в том числе и деревья.
• · Граф является двудольным в том и только в том случае, если он не содержит циклов нечетной длины.
• · Жадная раскраска показывает, что любой граф может быть окрашен при использовании на один цвет больше, чем его максимальная степень вершины,
• · Полные графы имеют и, графы-циклы имеют и, так что для них это ограничение является наилучшим, во всех других случаях, ограничение может быть улучшено; Теорема Брукса[11] утверждает, что

Теорема Брукса: для связанного, простого графа, если не является ни полный графом, ни графов-циклом.

Графы с большим хроматическим числом.

· Графы с большими кликами имеют большое хроматическое число, но обратное утверждение не всегда верно. Граф Грёча — это пример 4-раскрашиваемого графа без треугольников, и этот пример может быть обобщен на граф Мыцельского.

Теорема Мыцельского(Александр Зыков 1949, Jan Mycielski 1955): Существуют графы без треугольников со сколь угодно большими хроматическими числами.

· Из теоремы Брукса, графы с большим хроматическим числом должны иметь высокую максимальную степень вершины. Другое локальное условие, из-за которого хроматическое число может быть большим — это наличие большого клика. Но раскрашиваемость графа зависит не только от локальных условий: граф с большим обхватом локально выглядит как дерево, так все циклы длинные, но его хроматическое число не равно 2:

Теорема Эрдоса: Существуют графы со сколь угодно большим обхватом и хроматическим числом.

• · Рёберная раскраска — это раскраска вершин его линейного графа, и наоборот. То есть,
• · Более того,

Теорема Кёнига:, если — двудольный.

· В общем случае, связь намного сильнее, чем дает теорема Брукса для раскраски вершин:

Теорема Визинга: Граф с максимальной степенью вершины имеет реберное хроматическое число или .

Другие свойства.

• · Граф является k-хроматическим тогда и только тогда, когда он имеет ациклическую ориентацию, для которой длина наибольшего пути равна k. Это это было доказано в теореме Галлаи-Хассе-Роя-Витавера.
• · Для плоских графов, раскраска вершин эквивалентна везде-ненулевому потоку.
• · Об бесконечных графах известно намного меньше. Ниже приведены два результата для раскраски бесконечных графов.
• 1. Если все конечные подграфы бесконечного графа k-хроматические, то и тоже является k-хроматическим, по предположению аксиомы выбора. Это — формулировка теоремы Дэ Брейна-Эрдуша.
• 2. Если граф допускает полную n-раскраску для любого, то он допускает бесконечную полную раскраску.

Алгоритмы раскраски

Полиномиальные алгоритмы Для двудольного графа задача раскраски вычисляется за линейное время с помощью поиска в ширину. В случае совершенных графов, хроматическое число и соответствующая ему раскраска может быть найдена за полиномиальное время при использовании полуопределенного программирования. Приближенные формулы для нахождения хроматического числа известны для многих классов графов (леса, циклы, колеса, хордальные графы) и так же могут быть вычислены за полиномиальное время.

Точные алгоритмы Алгоритм полного перебора для случая k-раскраски рассматривает все комбинаций расстановки цветов в графе с n вершинами и проверяет их на корректность. Чтобы вычислить хроматическое число и хроматический полином данный алгоритм рассматривает каждое k, и может работать эффективно только для небольших графов.

Используя динамическое программирование и оценку размера наибольшего независимого множества в графе возможность k-раскраски может быть разрешена за время. Известны более быстрые алгоритмы для 3- и 4-раскрасок, сходящиеся за время и соответственно.

Сжатие Сжатие графа — это граф, полученный отождествлением вершин и, удаление соединяющих их ребер, замена на одну вершину, куда перенаправляются ребра инцидентные вершинам и. Эта операция играет важную роль в анализе раскраски графов.

Хроматическое число удовлетворяет рекуррентному соотношению:

.

где и несмежные вершины, граф с добавленным ребром. Некоторые алгоритмы основаны на данном соотношении, выдавая как результат дерево, иногда называемое деревом Зыкова. Время выполнения зависит от метода выбора вершин и .

Хроматический полином удовлетворяет рекуррентному соотношению:

.

где и смежные вершины, граф с удалением ребра. представляет собой число возможных правильных раскрасок графа, когда вершины могут иметь одинаковые или различные цвета. Если и имеют разные цвета, тогда мы можем рассмотреть граф, где и смежные. Если и имеют одинаковые цвета, мы можем рассмотреть граф, где и объединены.

Выражения данные выше приводят к рекурсивной процедуре, названной алгоритм удаления-сжатия, сформировавшей основу для многих алгоритмов раскраски графов. Время работы удовлетворяет такому же рекуррентному соотношению, как и числа Фибоначчи, поэтому в наихудшем случае алгоритм будет работать за время для n вершин и m ребер. На практике, метод ветвей и границ и отбрасывание изоморфных графов позволяет избежать некоторых рекурсивных вызовов, время работы зависит от метода подбора пары вершин.

Жадная раскраска.

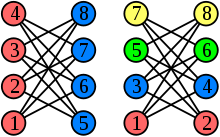
Два результата работы жадного алгоритма при выборе разных порядков вершин.

Жадный алгоритм упорядочивает вершины ,…, и последовательно присваивает вершине наименьший доступный цвет, не использовавшийся для окраски соседей среди ,…, либо добавляет новый. Качество полученной раскраски зависит от выбранного порядка. Всегда существует такой порядок, который приводит жадный алгоритм к оптимальному числу красок. С другой стороны, жадный алгоритм может быть сколь угодно плохим; например, корона с n вершинами может быть раскрашена 2 цветами, а упорядочивание может привести к числу цветов равному .

Для хордального графа и для его особых случаев (например, интервальный граф) алгоритм жадной раскраски может быть использован для нахождения оптимальной раскраски за полиномиальное время, выбирая порядок вершин обратным к совершенному порядку исключения. Однако найти такой порядок — NP-сложная задача для данного графа.

Если вершины упорядочены в соответствии с их степенями, алгоритм жадной раскраски использует не более чем цветов, как максимум на 1 больше чем (— степень вершины). Этот эвристический алгоритм иногда называют алгоритмом Уэлша-Пауэлла. Другой алгоритм устанавливает порядок динамично, выбирая следующую вершину той, которая имеет наибольшее число смежных вершин разных цветов. Многие другие алгоритмы раскраски графов основаны на жадной раскраске и используют статические или динамические стратегии выбора порядка вершин.

Параллельные и распределённые алгоритмы В области распределённых алгоритмов, раскраска графов тесно связана с проблемой нарушения симметрии. При достаточно большой максимальной степени вершин наиболее развитые вероятностные алгоритмы работают быстрее, чем детерминированные алгоритмы. Наиболее быстрые вероятностные алгоритмы используют технику множественных попыток.

В симметричных графах детерминированные распределённые алгоритмы не могут определить цвет вершины. Нужна дополнительная информация, чтобы избежать симметрии. Делается стандартное предположение, что первоначально каждая вершина имеет уникальный идентификатор, например, из множества. Пойдем от обратного, предположив, что нам дана n-раскраска. Задача состоит в том, чтобы уменьшить количество цветов от n до, например,. Чем больше цветов используются (вместо), тем меньше раундов связи требуется. Раунд связи подразумевает обмен узла произвольным сообщением с одним из своих соседей.

Простая версия распределённого жадного алгоритма дляраскраски требует раундов связи в худшем случае — информации, возможно, придется проходить из одной стороны сети в другую.

Наиболее простым интересным случаем является n-цикл. Ричард Коул и Узи Вишкин показывают, что существует распределённый алгоритм, который уменьшает количество цветов от n до в одном синхронном шаге связи. Повторяя ту же процедуру, можно получить 3-раскраску n-цикла за раундов связи (при условии, что мы имеем уникальные идентификаторы узлов).

Функция, итерированный логарифм, является чрезвычайно медленно растущей функцией, «почти константа». Следовательно, результаты Коула и Вишкина поднимают вопрос о том, есть ли распределённый алгоритм 3-раскраски n-цикла, который выполняется за константное время. Натан Линиал показал, что это не возможно: любой детерминированный распределённый алгоритм требует раундов связи для уменьшения N-раскраски до 3-раскраски в n-цикле.

Техника Коула и Вишкина также может быть применена для произвольного графа с ограниченной степенью вершин, в этом случае время работы составляет. Этот метод был обобщен для графа единичных кругов Шнайдером и др.

Проблема раскраски ребер также изучалась в распределённой модели. Пансонецци и Рицци достиглираскраски за в этой модели. Нижняя граница для распределённой раскраски вершин достигнутая Линиалом также применима для задачи распределённой раскраски ребер.

Децентрализованные алгоритмы Децентрализованными называются алгоритмы, в которых не разрешена внутренняя передача сообщений (в отличии от распределённых алгоритмов, где процессы обмениваются между собой данными). Существуют эффективные децентрализованные алгоритмы, успешно справляющиеся с задачей раскраски графов. Эти алгоритмы работают в предположении, что вершина способна «чувствовать», что какая-либо из её соседних вершин раскрашена в тот же цвет, что и она. Другими словами, есть возможность определить локальный конфликт. Такое условие довольно часто выполняется в реальных прикладных задачах — например, при передаче данных по беспроводному каналу передающая станция, как правило, имеет возможность детектировать, что другая станция пытается передавать одновременно в тот же канал. Способность к получению подобной информации является достаточным условием того, что алгоритмы основанные на обучающихся автоматах с единичной вероятностью правильно решат задачу раскраски графа.

Сложность вычислений Раскраска графа является вычислительно сложной задачей. Считается, что узнать допускает ли граф k-раскраску для заданного k — это NP-полная задача, кроме случаев k = 1 и k = 2. В частности, задача вычисления хроматического числа NP-сложна. Задача о 3-раскраске NP-полная даже для случая планарного графа степени 4.

Также NP-сложной задачей является раскраска 3-раскрашиваемого графа 4 цветами и k-раскрашиваемого графа при достаточно больших значениях k.

Вычисление коэффициентов хроматического полинома #P-сложная задача. Не существует на данный момент ни одного FPRAS для вычисления хроматического полинома ни для какого рационального числа k? 1,5, кроме k = 2, если только не выполнится, что NP = RP.