Лекция 5. Плоскопараллельное движение твердого тела

Плоскопараллельным или плоским называется такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости.

Пример 1. Качение цилиндра (катка) по неподвижной плоскости (рис. 1.1).

Выберем неподвижную систему координат так, чтобы каток катился основанием параллельно плоскости: .

Пример 2. Кривошипный механизм (рис. 1.2).

Кривошип ОА кривошипного механизма совершает вращательное движение вокруг неподвижной точки О. Кривошип соединен шарнирно в точке А с шатуном АВ, совершающим плоскопараллельное движение, и приводящим в движение ползун В.

Пусть тело совершает плоско-параллельное движение, и все его точки перемещаются в плоскостях, параллельных плоскости (рис. 1.3). Обозначим ее П₁. Построим плоскость П параллельно плоскости П₁ и пусть s — сечение тела плоскостью П. Тогда согласно определению сечение s будем двигаться в плоскости П. Проведем любую прямую АВ в теле, перпендикулярно плоскости П₁. Из определения плоского движения и из свойств твердого тела прямая АВ будет двигаться параллельно самой себе, т. е. поступательно. Тогда из теоремы о поступательном движении все точки прямой АВ будут двигаться одинаково. Следовательно, если будем знать движение сечения s, то будем знать и движение всего тела. Поэтому изучение плоскопараллельного движения сводится к изучению плоского сечения — движению плоской фигуры в своей плоскости.

Уравнения плоского движения

Пусть в неподвижной плоскости задано сечение тела s, совершающего плоское движение (рис. 9.4). Выберем произвольную точку О и скрепим жестко в этой точке подвижную систему координат. Точку О называют полюсом. Положение сечения s будет определяться положением координатных осей, а их положение определяется координатами полюса и углом. Зададим эти параметры как функции времени и получим уравнения плоскопараллельного движения:

,.

При этом число степеней свободы равно К=3.

Разложение плоского движения твердого тела на два простых движения — поступательное и вращательное

Вернемся к рис. 1.4 и введем вспомогательную подвижную систему координат, совершающую поступательное движение относительно системы координат. При поступательном движении осей оси будут совершать по отношению к ним вращательное движение вокруг полюса. Как известно для задания поступательного движения тела достаточно задать движения одной его точки, т. е. движение полюса О определяет поступательное движение осей :

.

Примем это движение за переносное. Тогда вращательное движение осей относительно подвижных осей, определяемое уравнением будет относительным.

От выбора полюса О вид функции зависит существенным образом, а вид функции (9.3) от выбора точки О не зависит. Покажем это.

Возьмем для наглядности прямоугольную фигуру. На рис 9.5 изображено начальное положение фигуры а) прямоугольника АВ и конечное положение б). Выберем сначала за полюс точку А и переместим прямоугольник АВ из положения а) в положение В сначала параллельным переносом (положение), а затем поворотом вокруг полюса А на угол. Затем выберем за полюс точку В и переместим прямоугольник АВ из положения а) в положение б) параллельным переносом в положение, затем поворотом вокруг полюса В на угол. Из рисунка видно, что по величине и откладываем угол в обоих случаях в одном направлении — по ходу часовой стрелки.

Вывод:

Введение

м вспомогательной системы координат плоское движение оказывается разложенным на два следующих движение: переносное — поступательное движение вместе с вспомогательной системой координат (определяется движением полюса) и относительное — вращательное движение подвижной плоскости вместе с плоской фигурой вокруг полюса (определяется углом поворота ).

При этом, поскольку выбор полюса произволен, то указанное разложение может быть выполнено бесчисленным множеством способов. Однако, во всех таких разложениях относительное вращательное движение остается одним и тем же, так как уравнение от выбора полюса не зависят.

Распределение скоростей при плоском движении

Вернемся к рис. 1.4 Определим скорость произвольной точки М плоской фигуры относительно осей в заданный момент времени.

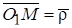
Введем векторы, , (рис. 1.6). Очевидно, что .

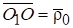
Рассмотрим движение точки М как сложное, состоящее из переносного поступательного движения плоской фигуры вместе с осями и относительного движения точки, которое будет происходить так, как двигаются точки тела, вращающегося вокруг оси, направленной перпендикулярной плоскости рисунка на читателя. Тогда скорость точки М относительно неподвижной системы координат является абсолютной скоростью и определяется по теореме сложения скоростей.

.

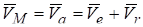
Пусть (m) — точка подвижной плоскости, с которой совпадает в заданный момент времени точка плоской фигуры М. Тогда, так как переносное движение поступательное, то.

.

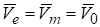
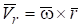
Относительная скорость точки от вращательного движения плоской фигуры вокруг оси (или относительно полюса О) по формуле Эйлера равна и следовательно,.

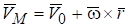
или.

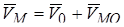
. (9.4).

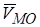
В формуле (1.4) символическая запись означает «скорость точки М от вращательного движения вокруг точки О» .

Таким образом, скорость произвольной точки плоской фигуры в некоторый момент времени равна геометрической сумме скорости полюса и скорости рассматриваемой точки в относительном вращательном движении плоской фигуры вокруг полюса.

Покажем, как найти скорость точки тела в заданный момент времени по формуле, если задан закон плоского движения:

,.

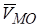
По первым формулам (9.5), определяющим закон движения полюса О, определим вектор по величине и направлению (рис. 9.7). По третьей формуле (9.5) определим угловую скорость плоской фигуры. Пусть вращение происходит по часовой стрелке. По модулю. Направим вектор перпендикулярно ОМ в сторону вращения плоской фигуры. Вектор скорости точки М получим, сложив векторы и по правилу параллелограмма.

Мгновенный центр скоростей

Формула (9.4) существенно упрощается, если в качестве полюса выбрать в рассматриваемый момент времени такую точку подвижной плоскости жестко связанной с плоской фигурой, скорость которой равна нулю. Такая точка носит название мгновенного центра скоростей. Обозначим ее — Р. Точка Р не обязательно принадлежит плоской фигуре. Она принадлежит подвижной плоскости .

Теорема: Если в некоторый момент времени плоское движение тела таково, что, то.

• 1. Мгновенный центр скоростей существует и он единственный.
• 2. Распределение скоростей в данный момент времени таково, как если бы тело совершало вращательное движение вокруг оси, проходящей через мгновенный центр скоростей.

Доказательство:

Пусть для определенности и существует точка А, скорость которой не равна нулю в заданный момент времени (иначе точка А — мгновенный центр скоростей) (рис. 1.8). Повернем вектор на 90 в направлении дуговой стрелки () и отложим на этом луче отрезок.

.

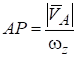
Так как, то АР — конечное число. Возьмем точку А в качестве полюса и вычислим скорость точки Р по формуле:

.

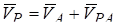
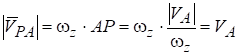
где .

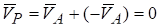
А так как, то .

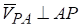
Итак, и точка Р — мгновенный центр скоростей. Из построения видно, что эта точка единственная.

2. Примем точку Р за полюс. Тогда формула будет иметь вид

.

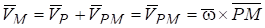
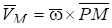
Следовательно, .

Теорема доказана.

Способы отыскания мгновенного центра скоростей

Рассмотрим некоторые частные случаи. На рис. 1.8 — 1.10 показаны способы нахождения мгновенного центра скоростей по скоростям двух точек плоскости фигуры. На рис. 1.8 известен вектор скорости, точки А и прямая, по которой направлен вектор скорости точки В.

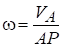
Мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям, восстановленным в этих точках. Угловая скорость щ находится по известной величине скорости: .

В случае, показанном на рис. 1.9 угловую скорость можно найти, пользуясь свойством пропорции, по одной из формул:

.

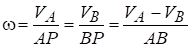
В случае, показанном на рис. 1.10, угловую скорость можно определить по формулам:

.

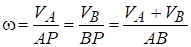
В случае, когда скорости точек А и В плоской фигуры параллельны, но не перпендикулярны к АВ (рис. 1.11), мгновенный центр скоростей находится в бесконечности и, следовательно, угловая скорость равна нулю. Векторы скоростей всех точек плоской фигуры в данный момент времени будут равны:

.

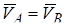
Движение плоской фигуры в этом случае в данный момент времени называют мгновенно поступательным.

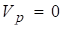
При качении без скольжения одного цилиндрического тела по поверхности другого (рис. 1.12) мгновенный центр скоростей совпадает с точкой соприкосновения тле, так как при отсутствии скольжения. Угловую скорость тела в этом случае можно вычислить по формуле.

.
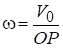