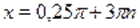Нестандартные тригонометрические уравнения

Использование ограниченности функций В практике централизованного тестирования не так уж редко встречаются уравнения, решение которых основывается на ограниченности функций и. Например:

Пример Решить уравнение .

Решение. Поскольку, , то левая часть не превосходит и равна, если.

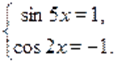
Для нахождения значений, удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них, затем среди найденных значений отберем те, которые удовлетворяют и другому.

Начнем со второго:,. Тогда ,.

.

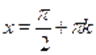
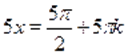
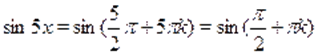
Понятно, что лишь для четных будет .

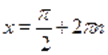
Ответ. .

Другая идея реализуется при решении следующего уравнения:

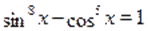
Пример Решить уравнение .

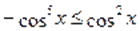
Решение. Воспользуемся свойством показательной функции:, .

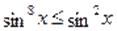
Сложив почленно эти неравенства будем иметь:

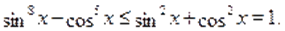
Следовательно левая часть данного уравнения равна тогда и только тогда, когда выполняются два равенства:

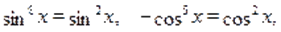
т. е. может принимать значения, ,, а может принимать значения, .

Ответ., .

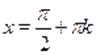
Пример Решить уравнение .

Решение.,. Следовательно,.

.

Ответ. .

Пример Решить уравнение.

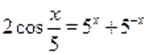
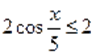
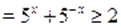
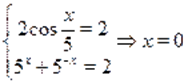
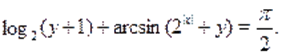
Решение. Обозначим, тогда из определения обратной тригонометрической функции имеем и .

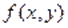
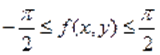
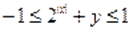
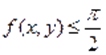
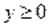
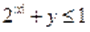
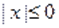
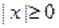
Так как, то из уравнения следует неравенство, т. е.. Поскольку и, то и. Однако и поэтому .

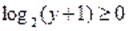
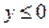
Если и, то. Так как ранее было установлено, что, то .

Ответ., .

Пример Решить уравнение.

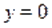
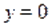
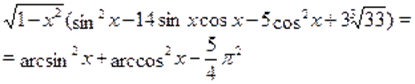
Решение. Областью допустимых значений уравнения являются .

Первоначально покажем, что функция.

при любых может принимать только положительные значения.

Представим функцию следующим образом:

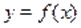
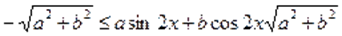
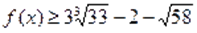
Поскольку, то имеет место, т. е. .

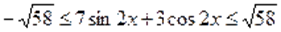
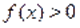
Следовательно, для доказательства неравенства, необходимо показать, что. С этой целью возведем в куб обе части данного неравенства, тогда.

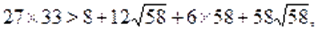
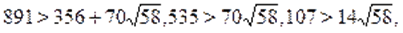
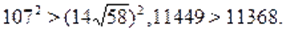
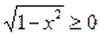
Полученное численное неравенство свидетельствует о том, что. Если при этом еще учесть, что, то левая часть уравнения неотрицательна.

Рассмотрим теперь правую часть уравнения .

Так как, то.

.

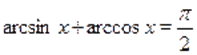
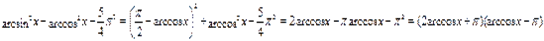
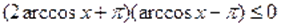
Однако известно, что. Отсюда следует, что, т. е. правая часть уравнения не превосходит. Ранее было доказано, что левая часть уравнения неотрицательна, поэтому равенство в может быть только в том случае, когда обе его части равны, а это возможно лишь при .

Ответ. .

Пример Решить уравнение.

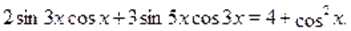
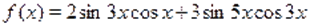
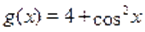
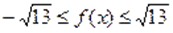
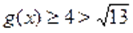
Решение. Обозначим и. Применяя неравенство Коши-Буняковского, получаем. Отсюда следует, что. C другой стороны имеет место. Следовательно, уравнение не имеет корней.

Ответ. .

Пример Решить уравнение:

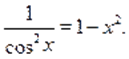
Решение. Перепишем уравнение в виде:

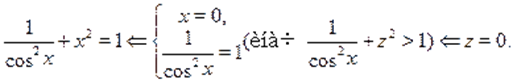
Ответ. .

Функциональные методы решения тригонометрических и комбинированных уравнений.

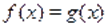
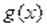
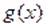
Не всякое уравнение в результате преобразований может быть сведено к уравнению того или иного стандартного вида, для которого существует определенный метод решения. В таких случаях оказывается полезным использовать такие свойства функций и, как монотонность, ограниченность, четность, периодичность и др. Так, если одна из функций убывает, а вторая возрастает на промежутке, то при наличии у уравнения корня на этом промежутке, этот корень единственный, и тогда его, например, можно найти подбором. Если же функция ограничена сверху, причем, а функция ограничена снизу, причем, то уравнение равносильно системе уравнений.

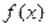
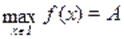
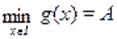
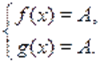
Пример Решить уравнение.

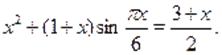
Решение. Преобразуем исходное уравнение к виду.

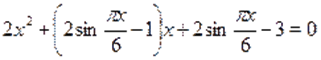
и решим его как квадратное относительно. Тогда получим,.

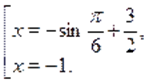
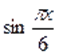
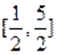
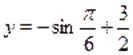
Решим первое уравнение совокупности. Учтя ограниченность функции, приходим к выводу, что уравнение может иметь корень только на отрезке. На этом промежутке функция возрастает, а функция убывает. Следовательно, если это уравнение имеет корень, то он единственный. Подбором находим .

Ответ. .

Пример Решить уравнение.

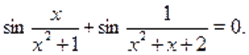
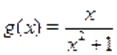
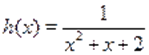
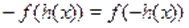
Решение. Пусть, и, тогда исходное уравнение можно записать в виде функционального уравнения. Поскольку функция нечетная, то. В таком случае получаем уравнение .

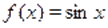
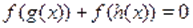
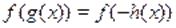
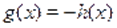
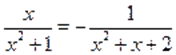
Так как, и монотонна на, то уравнение равносильно уравнению, т. е., которое имеет единственный корень .

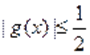
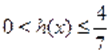
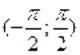
Ответ. .

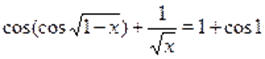
Пример Решить уравнение .

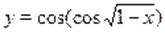
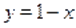
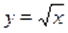
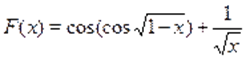
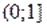
Решение. На основании теоремы о производной сложной функции ясно, что функция убывающая (функция убывающая, возрастающая, убывающая). Отсюда понятно, что функция определенная на, убывающая. Поэтому данное уравнение имеет не более одного корня. Так как, то.

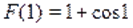
Ответ. .

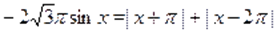
Пример Решить уравнение .

Решение. Рассмотрим уравнение на трех промежутках.

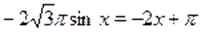
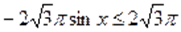
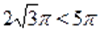
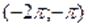
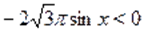
а) Пусть. Тогда на этом множестве исходное уравнение равносильно уравнению. Которое на промежутке решений не имеет, т. к., , а. На промежутке исходное уравнение так же не имеет корней, т. к., а .

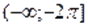
б) Пусть. Тогда на этом множестве исходное уравнение равносильно уравнению.

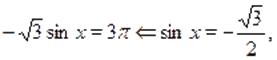
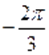
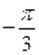
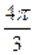
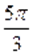
корнями которого на промежутке являются числа, ,, .

в) Пусть. Тогда на этом множестве исходное уравнение равносильно уравнению.

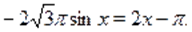
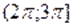
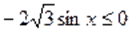
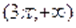
Которое на промежутке решений не имеет, т. к., а. На промежутке уравнение так же решений не имеет, т. к., , а .

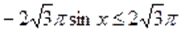
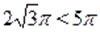
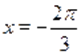
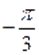
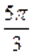
Ответ., ,, .

Метод симметрии Метод симметрии удобно применять, когда в формулировке задания присутствует требование единственности решения уравнения, неравенства, системы и т. п. или точное указание числа решений. При этом следует обнаружить какую-либо симметрию заданных выражений.

Нужно также учитывать многообразие различных возможных видов симметрии.

Не менее важным является четкое соблюдение логических этапов в рассуждениях с симметрией.

Обычно симметрия позволяет установить лишь необходимые условия, а затем требуется проверка их достаточности.

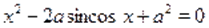
Пример Найти все значения параметра, при которых уравнение имеет единственное решение.

Решение. Заметим, что и —- четные функции, поэтому левая часть уравнения есть четная функция.

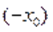
Значит если —- решение уравнения, то есть также решение уравнения. Если —- единственное решение уравнения, то, необходимо, .

Отберем возможные значения, потребовав, чтобы было корнем уравнения.

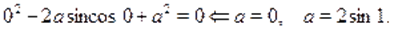
Сразу же отметим, что другие значения не могут удовлетворять условию задачи.

Но пока не известно, все ли отобранные в действительности удовлетворяют условию задачи.

Достаточность.

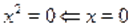
• 1), уравнение примет вид .
• 2), уравнение примет вид:

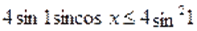
Очевидно, что, для всех и. Следовательно, последнее уравнение равносильно системе:

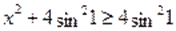
Тем самым, мы доказали, что при, уравнение имеет единственное решение.

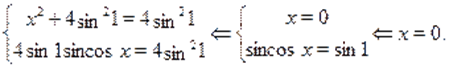
Ответ. .

Решение с исследованием функции Пример Докажите, что все решения уравнения.

—- целые числа.

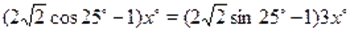
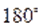
Решение. Основной период исходного уравнения равен. Поэтому сначала исследуем это уравнение на отрезке .

Преобразуем уравнение к виду:

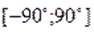
При помощи микрокалькулятора получаем:

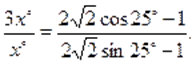
Находим:

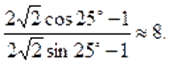
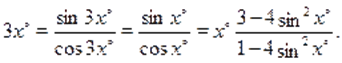
Если, то из предыдущих равенств получаем:

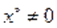
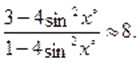
Решив полученное уравнение, получим: .

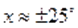
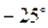
Выполненные вычисления представляют возможность предположить, что корнями уравнения, принадлежащими отрезку, являются, и .

Непосредственная проверка подтверждает эту гипотезу. Таким образом, доказано, что корнями уравнения являются только целые числа, .

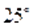
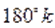
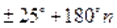
Пример Решите уравнение .

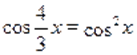
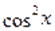
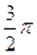
Решение. Найдём основной период уравнения. У функции основной период равен. Основной период функции равен. Наименьшее общее кратное чисел и равно. Поэтому основной период уравнения равен. Пусть .

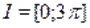
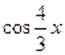
Очевидно, является решением уравнения. На интервале. Функция отрицательна. Поэтому другие корни уравнения следует искать только на интервалаx и .

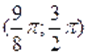
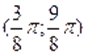
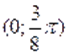
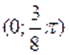
При помоши микрокалькулятора сначала найдем приближенные значения корней уравнения. Для этого составляем таблицу значений функции на интервалах и; т. е. на интервалах и .

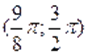
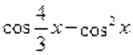
• 0
• 0
• 202,5
• 0,85 355 342
• 3
• -0,80 306
• 207
• 0,6 893 642
• 6
• -0,119 426
• 210
• 0,57 635 189
• 9
• -0,261 932
• 213
• 0,4 614 465
• 12
• -0,448 897
• 216
• 0,34 549 155
• 15
• -0,667 995
• 219
• 0,22 934 931
• 18
• -0,903 692
• 222
• 0,1 138 931
• 21
• -0,1 137 519
• 225
• 0,2
• 24
• -0,1 312 438
• 228
• -0,11 145 712
• 27
• -0,1 512 438
• 231
• -0,21 961 736
• 30
• -0,1 604 446
• 234
• -0,32 363 903
• 33
• -0,1 597 149
• 237
• -0,42 270 819
• 36
• -0,1 462 203
• 240
• -0,5 160 445
• 39
• -0,1 170 562
• 243
• -0,60 290 965
• 42
• -0,692 866
• 246
• -0,65 261 345
• 45
• 0,2
• 249
• -0,75 452 006
• 48
• 0,936 458
• 252
• -0,81 805 397
• 51
• 0,2 143 757
• 255
• -0,87 270 535
• 54
• 0,3 647 455
• 258
• -0,91 803 444
• 57
• 0,547 098
• 261
• -0,95 367 586
• 60
• 0,7 635 185
• 264
• -0,97 934 187
• 63
• 0,10 157 893
• 267
• -0,99 482 505
• 66
• 0,1 305 352
• 270
• -1
• 67,5
• 0,14 644 661

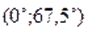
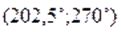
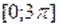
Легко усматриваются следующие гипотезы: корнями уравнения, принадлежащими отрезку, являются числа:; ;. Непосредственная проверка подтверждает эту гипотезу.

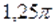
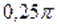
Ответ.;; .