Учебный модуль 9. Теория вероятности

Тема 21. Дискретные случайные величины. Дискретная случайная величина. Математическое ожидание, дисперсия, среднее квадратичное отклонение, их свойства. Биноминальный закон распределения и закон Пуассона. Элементы теории массового обслуживания. Закон больших чисел

Дискретные случайные величины. Математическое ожидание, дисперсия, среднее квадратичное отклонение. Биноминальный закон распределения и закон Пуассона. Элементы теории массового обслуживания.

Определение случайной величины. Величина, которая в результате опыта может принимать одно и только одно определенное значение, до опыта не известное и зависящее от причин, которые нельзя учесть заранее, называется случайной величиной. Случайные величины обычно обозначают заглавными буквами: X, Y, Z, …, а их возможные значения — прописными буквами: х, y, z, … Понятие случайной величины обобщает понятие случайного события.

Например:

• 1. Выпадение пяти очков при бросании игрального кубика — случайное событие. Случайная величина — число выпавших очков .
• 2. Исследуется надежность нового прибора. Случайным событием является факт прохождения тестовых испытаний (прибор удовлетворяет — не удовлетворяет оговоренному уровню требований). Случайной величиной является процент приборов прошедших испытание.

Если множество значений случайной величины конечно или счетно, то случайная величина называется дискретной. Дискретная принимает отдельные значения, причем эти возможные значения можно пронумеровать. Примеры дискретных величин: количество клиентов; количество диалектов в данном языке; количество включений аппаратуры до первого отказа и т. п.

Cоотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями их появления, называется законом распределения случайной величины.

Для дискретной случайной величины законом распределения выступает правило сопоставляющее каждому возможному значению хi случайной величины X вероятность его появления.

pi = P(X = хi). Последнее выражение читается так: «вероятность того, что случайная величина X примет значение хi». Для дискретной случайной величины закон распределения проще всего задавать в виде таблицы.

Так как случайная величина обязательно примет одно из своих значений, то.

(19.1).

Пример. Дискретная случайная величина имеет закон распределения:

Найти: р.

Решение. Так как 0,1 + 0,2 + 0,2 + р = 1, то р = 1 — 0,5 = 0,5.

При решении многих задач достаточно знание лишь основных числовых характеристик случайных величин. К таким характеристикам в первую очередь относятся: математическое ожидание, дисперсия и среднее квадратичное (квадратическое) отклонение.

Математическим ожиданием для дискретной случайной величины называется сумма произведений значений случайной величины на соответствующие им вероятности. Математическое ожидание называют также средним вероятностным. Математическое ожидание вычисляется по формуле.

Математическое ожидание можно рассматривать как среднее вероятностное значениеслучайной величины, учитывая, что каждое возможное значение входит со своим «весом», которым и является вероятность. является центром распределения возможных значений рассматриваемой случайной величины. Если все значения равновероятны, то математическое ожидание будет равно среднему арифметическому всех возможных значений:

.

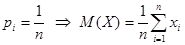
В приведенной выше формуле случайная величина принимает конечное число значений. Если число значений бесконечно, то.

.

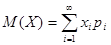
при этом математическое ожидание существует, если ряд в правой части этой формулы абсолютно сходится.

Пример. В магазин ежедневно поступает не более пяти компьютеров. Известны вероятности их поступления.

Найти математическое ожидание числа поступлений компьютеров.

Решение. Закон распределения вероятностей.

.

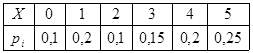
Свойства математического ожидания.

Математическое ожидание постоянной величины равно этой постоянной. Действительно, постоянная величина принимает только одно значение С с вероятностью равной 1.

Постоянный множитель можно выносить за знак математического ожидания.

Доказательство.

Если — случайная величина, которая принимает значения с вероятностями, т. е. с вероятностями значений. Тогда математическое ожидание величины.

.

Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий.

Доказательство. Докажем для суммы двух случайных величин.

.

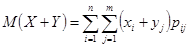
Раскроем скобки и разобьем это выражение на две части:

.

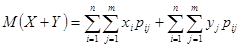
В первой двойной сумме не зависит от индекса, по которому ведется суммирование во второй сумме, и, аналогично во второй сумме не зависит от индекса, то.

.

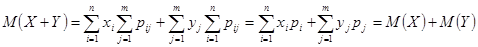
Следствие 1. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю.

Действительно,.

.

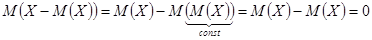
Следствие 2. Математическое ожидание разности случайных величин равно разности математических ожиданий.

Это свойство является следствием второго и третьего свойств.

Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий.

Доказательство. По определению произведене случайных величин представляет собой случайную величину, которая принимает все значения.

с вероятностями.

(так как независимы). Поэтому.

.

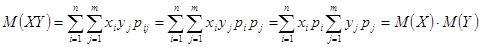
Пример. Пусть и — независимые случайные величины с математическими ожиданиями.

.

Найти математическое ожидание случайной величины.

.