Решение.
Дискретные случайные величины.
Закон Пуассона

Пример. Для продвижения своей продукции на рынок фирма раскладывает по почтовым ящикам рекламные листки. Прежний опыт работы показывает, что примерно в одном случае из 2 000 следует заказ. Найти вероятность того, что при размещении 10 000 рекламных листков поступит хотя бы один заказ, среднее число поступивших заказов и дисперсию числа поступивших заказов. Пример 3. Два равносильных спортсмена… Читать ещё >
Решение. Дискретные случайные величины. Закон Пуассона (реферат, курсовая, диплом, контрольная)
В качестве меры рассеивания значений случайной величины используется дисперсия
(или).
Дисперсия (слово дисперсия означает «рассеяние») есть мера рассеивания значений случайной величины относительно ее математического ожидания. Дисперсией называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
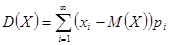
(19.3).
Если случайная величина — дискретная с бесконечным, но счетным множеством значений, то.
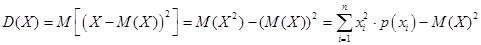
.
если ряд в правой части равенства сходится.
Свойства дисперсии.
- 1. Дисперсия постоянной величины равна нулю
- 2. Дисперсия суммы случайных величин равна сумме дисперсий
- 3. Постоянный множитель можно выносить за знак дисперсии в квадрате
.
Дисперсия разности случайных величин равна сумме дисперсий
Это свойство является следствием второго и третьего свойств. Дисперсии могут только складываться.
Дисперсию удобно вычислять по формуле, которую легко получить, используя свойства дисперсии
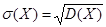
(19.4).
Дисперсия всегда величина положительная.
Дисперсия имеет размерность квадрата размерности самой случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину.
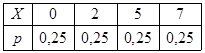
.
Средним квадратическим отклонением (стандартным отклонением или стандартом) случайной величиныназывается арифметическое значение корня квадратного из её дисперсии.
Пример 1.
Бросают две монеты достоинством 2 и 5 рублей. Если монета выпадает гербом, то начисляют ноль очков, а если цифрой, то число очков, равное достоинству монеты. Найти математическое ожидание и дисперсию числа очков.
Решение. Найдем вначале распределение случайной величины Х — числа очков. Все комбинации — (2;5),(2;0),(0;5),(0;0) — равновероятны и закон распределения:
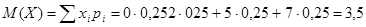
Математическое ожидание:
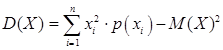
.
Дисперсию найдем по формуле.
.
для чего вычислим.
.
тогда .
Пример 2.
Найти неизвестную вероятность р, математическое ожидание и дисперсию дискретной случайной величины, заданной таблицей распределения вероятностей.
Х. | |||||
Р. | 0,0081. | 0,0756. | 0,2646. | 0,4116. | р |
Решение. Так как сумма всех вероятностей в таблице равна единице, то.
0,0081+0,0756+0,2646+0,4116 + р =1.
Отсюда р = 0,2401. Теперь можно написать закон распределения.
Х. | |||||
Р. | 0,0081. | 0,0756. | 0,2646. | 0,4116. | 0,2401. |
Находим математическое ожидание и дисперсию:
M(X) = 00,0081 + 10,0756 + 20,2646 + 3 0,4116 + +40,2401=2,8.
Для вычисления дисперсии воспользуемся формулой (19.4).
D(X) = 020, 0081 + 120,0756 + 220,2646 + 320,4116 + 420,2401 — 2,82 = 8,68 ;
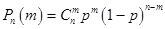
— 2,82 = 0,84.
Пример 3. Два равносильных спортсмена проводят турнир, который длится или до первой победы одного из них, или до тех пор, пока не будет сыграно пять партий. Вероятность победы в одной партии для каждого из спортсменов равна 0,3, а вероятность ничейного исхода партии 0,4. Найти закон распределения, математическое ожидание и дисперсию числа сыгранных партий.
Решение. Случайная величина Х — количество сыгранных партий, принимает значения от 1 до 5, т. е.
.
Определим вероятности окончания матча. Матч закончится на первой партии, если кто-то их спортсменов выиграл. Вероятность выигрыша равна.
Р(1) = 0,3+0,3 =0,6.
Если же была ничья (вероятность ничьей равна 1 — 0,6 = 0,4), то матч продолжается. Матч закончится на второй партии, если в первой была ничья, а во второй кто-то выиграл. Вероятность.
Р(2) = 0,4•0,6=0,24.
Аналогично, матч закончится на третьей партии, если было подряд две ничьи и опять кто-то выиграл.
Р(3) = 0,4•0,4•0,6 = 0,096. Р(4)= 0,4•0,4•0,4•0,6=0,0384.
Пятая партия в любом варианте последняя.
Р(5)= 1 — (Р(1)+Р(2)+Р(3)+Р(4)) = 0,0256.
Сведем все в таблицу. Закон распределения случайной величины «число выигранных партий» имеет вид.
0,6. | 0,24. | 0,096. | 0,0384. | 0,0256. |
Математическое ожидание Дисперсию вычисляем по формуле (19.4).
Стандартные дискретные распределения.
Биномиальное распределение. Пусть реализуется схема опытов Бернулли: проводится n одинаковых независимых опытов, в каждом из которых событие A может появиться с постоянной вероятностью p и не появится с вероятностью.
(см. лекцию 18).
Число появлений события A в этих n опытах есть дискретная случайная величина X, возможные значения которой:
0; 1; 2; …; m; … ; n.
Вероятность появления m событий A в конкретной серии из n опытов с и закон распределения такой случайной величины задается формулой Бернулли (см. лекцию 18).
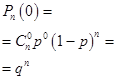
. (19.6).
X. | … | m. | … | n. | ||
P. | 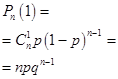 … | … |
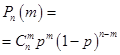
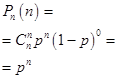
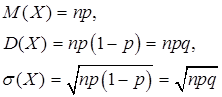
Числовые характеристики случайной величины X распределенной по биномиальному закону:
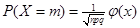
. (19.7).
Если n велико (), то, при, формула (19.6) переходит в формулу.
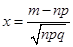
(19.8).
Где.
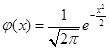
.
а табулированная функция Гаусса (таблица значений функции Гаусса приведена в конце 18 лекции).
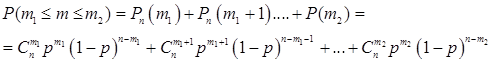
На практике часто важна не сама вероятность появления m событий A в конкретной серии из n опытов, а вероятность того, что событие А появится не менее.
раз и не более раз, т. е. вероятность того, что Х принимает значения.
от до .
Для этого надо просуммировать вероятности.
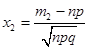
(19.9).
Если n велико (), то, при, формула (19.9) переходит в приближенную формулу.
(19.10).
где.
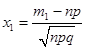
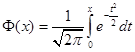
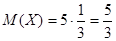
, а .
табулированная функция. Таблицы приведены в конце лекции 18.
При использовании таблиц надо учесть, что.
.
Пример 1. Автомобиль, подъезжая к перекрестку, может продолжить движение по любой из трех дорог: A, B или C с одинаковой вероятностью. К перекрестку подъезжают пять автомобилей. Найти среднее число автомашин, которое поедет по дороге A и вероятность того, что по дороге B поедет три автомобиля.
Решение. Число автомашин проезжающих по каждой из дорог является случайной величиной. Если предположить, что все подъезжающие к перекрестку автомобили совершают поездку независимо друг от друга, то эта случайная величина распределена по биномиальному закону с.
n = 5 и p = .
Следовательно, среднее число автомашин, которое проследует по дороге A, есть по формуле (19.7).
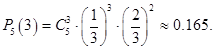
а искомая вероятность при.
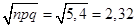
Пример 2. Вероятность отказа прибора при каждом испытании 0,1. Производится 60 испытаний прибора. Какова вероятность того, что отказ прибора произойдёт: а) 15 раз; б) не более 15 раз?
Решение.
а. Так как число испытаний 60, то используем формулу (19.8).
.
,.
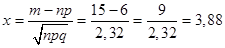
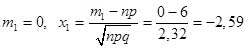
По таблице 1 приложения к лекции 18 находим.
б. Используем формулу (19.10).
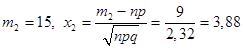
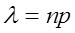
По таблице 2 приложения к лекции 18.
- — 0,495
- 0,49 995
Распределение Пуассона) закон редких явлений). Если n велико, а р мало (), при этом произведение пр сохраняет постоянное значение, которое обозначим л,.
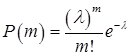
.
то формула (19.6) переходит в формулу Пуассона.
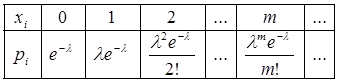
Закон распределения Пуассона имеет вид:
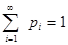
Очевидно, что определение закона Пуассона корректно, т.к. основное свойство ряда распределения.
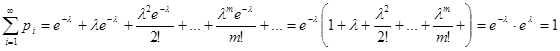
выполнено, т.к. сумма ряда.
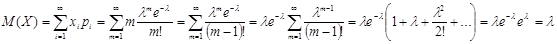
.
В скобках записано разложение в ряд функции при.
.
Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого закона, т. е.
.
Доказательство.
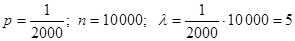
Пример. Для продвижения своей продукции на рынок фирма раскладывает по почтовым ящикам рекламные листки. Прежний опыт работы показывает, что примерно в одном случае из 2 000 следует заказ. Найти вероятность того, что при размещении 10 000 рекламных листков поступит хотя бы один заказ, среднее число поступивших заказов и дисперсию числа поступивших заказов.
Решение. Здесь.
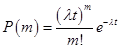
.
Отсюда.
.
Вероятность того, что поступит хотя бы один заказ, найдем через вероятность противоположного события, т. е.
.
Случайный поток событий. Потоком событий называется последовательность событий, происходящие в случайные моменты времени. Типичными примерами потоков являются сбои в компьютерных сетях, вызовы на телефонных станциях, поток заявок на ремонт оборудования и т. д.
Поток событий называется стационарным, если вероятность попадания того или иного числа событий на временной интервал длины зависит только от длины интервала и не зависит не зависит от расположения временного интервала на оси времени.
Условию стационарности удовлетворяет поток заявок, вероятностные характеристики которого не зависят от времени. В частности, для стационарного потока характерна постоянная плотность (среднее число заявок в единицу времени). На практике часто встречаются потоки заявок, которые (по крайней мере, на ограниченном отрезке времени) могут рассматриваться как стационарные. Например, поток вызовов на городской телефонной станции на участке времени от 12 до 13 часов может считаться стационарным. Тот же поток в течение целых суток уже не может считаться стационарным (ночью плотность вызовов значительно меньше, чем днем).
Поток событий называется потоком с отсутствием последействия, если для любых неперекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.
Условие отсутствия последействия — наиболее существенное для простейшего потока — означает, что заявки поступают в систему независимо друг от друга. Например, поток пассажиров, входящие на станцию метро, можно считать потоком без последействия потому, что причины, обусловившие приход отдельного пассажира именно в тот, а не другой момент, как правило, не связаны с аналогичными причинами для других пассажиров. Однако условие отсутствия последействия может быть легко нарушено за счет появления такой зависимости. Например, поток пассажиров, покидающих станцию метро, уже не может считаться потоком без последействия, так как моменты выхода пассажиров, прибывших одним и тем же поездом, зависимы между собой.
Поток событий называется ординарным, если вероятность попадания на малый интервал времени t двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события (в этой связи закон Пуассона называют законом редких событий).
Условие ординарности означает, что заявки приходят поодиночке, а не парами, тройками и т. д. дисперсия отклонение распределение бернулли Например, поток клиентов, входящих в парикмахерскую, может считаться практически ординарным. Если в неординарном потоке заявки поступают только парами, только тройками и т. д., то неординарный поток легко свести к ординарному; для этого достаточно вместо потока отдельных заявок рассмотреть поток пар, троек и т. д. Сложнее будет, если каждая заявка случайным образом может оказаться двойной, тройной и т. д. Тогда уже приходится иметь дело с потоком не однородных, а разнородных событий.
Если поток событий обладает всеми тремя свойствами (т. е. стационарен, ординарен и не имеет последействия), то он называется простейшим (или стационарным пуассоновским) потоком. Название «пуассоновский» связано с тем, что при соблюдении перечисленных условий число событий, попадающих на любой фиксированный интервал времени, будет распределено по закону Пуассона
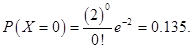
(19.11).
Здесь — среднее число событий A, появляющихся за единицу времени .
Этот закон однопараметрический, т. е. для его задания требуется знать только один параметр. Можно показать, что математическое ожидание и дисперсия в законе Пуассона численно равны:
Пример. Пусть в середине рабочего дня среднее число запросов равняется 2 в секунду. Какова вероятность того, что 1) за секунду не поступит ни одной заявки, 2) за две секунды поступит 10 заявок?
Решение. Поскольку правомерность применения закона Пуассона не вызывает сомнения и его параметр задан (= 2), то решение задачи сводится к применении формулы Пуассона (19.11).
1) t = 1, m = 0:
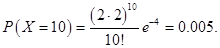
2) t = 2, m = 10:
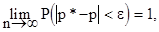
Закон больших чисел. Математическим основанием того факта, что значения случайной величины группируются около некоторых постоянных величин, является закон больших чисел.
Исторически первой формулировкой закона больших чисел стала теорема Бернулли:
" При неограниченном увеличении числа одинаковых и независимых опытов n частота появления события A сходится по вероятности к его вероятности", т. е.
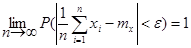
(19.10).
где частота появления события A в n опытах,.
р* = .
Содержательно выражение (19.10) означает, что при большом числе опытов частота появления события A может заменять неизвестную вероятность этого события и чем больше число проведенных опытов, тем ближе р* к р. Интересен исторический факт. К. Пирсон бросал монету 12 000 раз и герб у него выпал 6019 раз (частота 0.5016). При бросании этой же монеты 24 000 раз он получил 12 012 выпадений герба, т. е. частоту 0.5005.
Наиболее важной формой закона больших чисел является теорема Чебышева: при неограниченном возрастании числа независимых, имеющих конечную дисперсию и проводимых в одинаковых условиях опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию. В аналитической форме эта теорема может быть записана так:
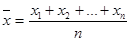
(19.11).
Теорема Чебышева кроме фундаментального теоретического значения имеет и важное практическое применение, например, в теории измерений. Проведя n измерений некоторой величины х, получают различные несовпадающие значения х1, х2, …, хn. За приближенное значение измеряемой величины х принимают среднее арифметическое наблюденных значений.
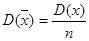
(19.12).
При этом, чем больше будет проведено опытов, тем точнее будет полученный результат. Дело в том, что дисперсия величины убывает с возрастанием числа проведенных опытов, т.к.
D(x1) = D(x2)=…= D(xn) D(x), то.
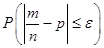
(19.13).
Соотношение (19.13) показывает, что и при высокой неточности приборов измерения (большая величина) за счет увеличения количества измерений можно получать результат со сколь угодно высокой точностью.
Используя формулу (19.10) можно найти вероятность того, что статистическая частота отклоняется от вероятности не более, чем на.
.
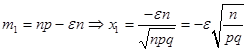
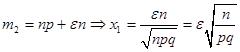
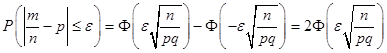
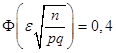
(19.14).
Пример. Вероятность события в каждом испытании равна 0,4. Сколько нужно провести испытаний, чтобы с вероятностью, не меньшей, чем 0,8 ожидать, что относительная частота события будет отклоняться от вероятности по модулю менее, чем на 0,01?
Решение. По формуле (19.14).
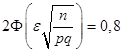
,.
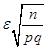
следовательно, по таблице два приложения.
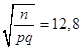
=1,28,, .
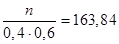
Или.
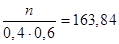
следовательно, n 3932.