Уравнения напряжений асинхронного двигателя

Как следует из принципа действия асинхронного двигателя (см. § 6.2), обмотка ротора не имеет электрической связи с обмоткой статора. Между этими обмотками существует только магнитная связь, и энергия из обмотки статора передается в обмотку ротора магнитным полем. В этом отношении асинхронная машина аналогична трансформатору: обмотка статора является первичной, а обмотка ротора — вторичной.

В процессе работы асинхронного двигателя токи в обмотках статора и ротора создают две магнитодвижущие силы; МДС статора и МДС ротора. Совместным действием эти МДС наводят в магнитной системе двигателя результирующий магнитный поток, вращающийся относительно статора с синхронной частотой вращения n₁. Так же как и в трансформаторе, этот магнитный поток можно рассматривать состоящим из основного потока Ф, сцепленного как с обмоткой статора, так и с обмоткой ротора (магнитный поток взаимоиндукции), и двух потоков рассеяния: Ф_у1 — потока рассеяния обмотки статора и Ф _у2 — потока рассеяния обмотки ротора (см. § 11.3). Рассмотрим, какие ЭДС наводят указанные потоки в обмотках двигателя.

Электродвижущие силы, наводимые в обмотке статора. Основной магнитный поток Ф, вращающийся с частотой n₁ наводит в неподвижной обмотке статора ЭДС Е₁, значение которой определяется выражением [см. (7.20)] E₁ = 4,44 f₁ Ф щ₁ k_об1.

Магнитный поток рассеяния Ф_у1 наводит в обмотке статора ЭДС рассеяния, значение которой определяется индуктивным падением напряжения в обмотке статора:

у1 = - j1x1 (12.1).

где х₁ — индуктивное сопротивление рассеяния фазной обмотки статора [см. (11.6)], Ом.

Для цепи обмотки статора асинхронного двигателя, включенной в сеть с напряжением U₁, запишем уравнение напряжений по второму закону Кирхгофа:

₁ + ₁ + _у1 = ₁ r₁, (12.2).

где I₁ r₁ — падение напряжения в активном сопротивлении обмотки статора r₁.

После переноса ЭДС E₁, и E_у1, в правую часть уравнения (12.2) с учетом (12.1) получим уравнение напряжений обмотки статора асинхронного двигателя:

₁ = (-₁) + j ₁ x₁ + ₁r₁ (12.3).

Сравнив полученное уравнение с уравнением (1.13), видим, что оно не отличается от уравнения напряжений для первичной цепи трансформатора.

Электродвижущие силы, наводимые в обмотке ротора. В процессе работы асинхронного двигателя ротор вращается в сторону вращения поля статора с частотой n₂. Поэтому частота вращения поля статора относительно ротора равна разности частот вращения (n₁ — n₂). Основной магнитный поток Ф, обгоняя ротор с частотой вращения n_s = (n₁ — n₂), индуцирует в обмотке ротора ЭДС Е2 = 4,44 f2 Ф щ2 коб2 (12.4).

где f₂— частота ЭДС Е_2s в роторе, Гц; щ₂ — число последовательно соединенных витков одной фазы обмотки ротора; k_o62 — обмоточный коэффициент обмотки ротора.

Частота ЭДС (тока) в обмотке вращающегося ротора пропорциональна частоте вращения магнитного поля относительно ротора n_s = n₁ — n₂, называемой частотой скольжения:

f₂ = pn_s / 60 = p (n₁ — n₂) / 60,

или.

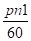
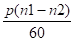
т. е. частота ЭДС (тока) ротора пропорциональна скольжению. Для асинхронных двигателей общепромышленного назначения эта частота обычно невелика и при f₁ = 50 Гц не превышает нескольких герц, так при s = 5% частота f₂ = 50 0,05 = 2,5 Гц. Подставив (12.5) в (12.4), получим.

E_2s = 4,44 f₁ s Ф щ₂ k_об2 = E₂ s. (12.6).

Здесь Е₂ — ЭДС, наведенная в обмотке ротора при скольжении s = 1, т. е. при неподвижном роторе, В.

Поток рассеяния ротора Ф_у2 индуцирует в обмотке ротора рассеяния, значение которой определяется индуктивным падением напряжения в этой обмотке:

у2 = - j2 x2 s (12.7).

где х₂ — индуктивное сопротивление рассеяния обмотки ротора при неподвижном роторе [см. (11.8)], Ом.

Обмотка ротора асинхронного двигателя электрически не связана с внешней сетью и к ней не подводится напряжение. Ток в этой обмотке появляется исключительно за счет ЭДС, наведенной основным магнитным потоком Ф. Поэтому уравнение напряжений для цепи ротора асинхронного двигателя по второму закону Кирхгофа имеет вид.

_2s + _у2 = ₂ r₂

где r₂ — активное сопротивление обмотки ротора. С учетом (12.6) и (12.7) получим.

_2s — j₂ x₂ s —₂ r₂ (12.8).

Разделив все слагаемые равенства (12.8) на s, получим.

• 2 — j₂ x₂ —₂ r₂ / s = 0 (12.9)
• -уравнение напряжений для обмотки ротора.

Уравнения МДС и токов асинхронного двигателя Основной магнитный поток Ф в асинхронном двигателе создается совместным действием МДС обмоток статора F₁ и ротора F₂:

= (1 + 2) / Rм = 0 / Rм (12.10).

где R_м — магнитное сопротивление магнитной цепи двигателя потоку Ф; F₀ — результирующая МДС двигателя, численно равная МДС обмотки статора в режиме х.х. [см. (9.16)]:

F₀ = 0,45m₁ I₁ щ₁ k_об1/ P (12.11).

I₀ — ток х.х. в обмотке статора, А.

МДС обмоток статора и ротора на один полюс в режиме нагруженного двигателя.

F₁ = 0,45 m₁ I₁ щ₁ k_об1/ P

F₂ = 0,45 m₂ I₂ щ₂ k_об2/ P (12.2).

где m₂ — число фаз в обмотке ротора; k_o62 — обмоточный коэффициент обмотки ротора.

При изменениях нагрузки на валу двигателя меняются токи в статоре I₁, и роторе I₂. Но основной магнитный поток Ф при этом сохраняется неизменным, так как напряжение, подведенное к обмотке статора, неизменно (U₁ = const) и почти полностью уравновешивается ЭДС Е₁ обмотки статора [см. (12.3)]:

₁ ? (-₁) (12.13).

Так как ЭДС Е₁ пропорциональна основному магнитному потоку Ф [см. (7.20)], то последний при изменениях нагрузки остается неизменным. Этим и объясняется то, что, несмотря на изменения МДС F₁ и F₂, результирующая МДС остается неизменной, т. е. ₀ = ₁ + ₂ = const.

Подставив вместо F₀, F₁ и F₂ их значения по (12.11) и (12.12), получим.

0,45 m_{1 0} щ₁ k_об1/ p = 0,45m_{1 1} щ₁ k_об1/ p + 0,45 m_{2 2} щ₂ k_o62/ р.

Разделив это равенство на m₁ щ₁ k_об1/ p, определим уравнение токов асинхронного двигателя:

₀ = ₁ + ₂ =₁ + ^?₂ (12.14).

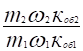
где.

^?₂=₂ (12.15).

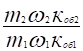
— ток ротора, приведенный к обмотке статора.

Преобразовав уравнение (12.14), получим уравнение токов статора асинхронного двигателя.

₁ =₀ + (-^?₂) (12.16).

из которого следует, что ток статора в асинхронном двигателе ₁ имеет две составляющие: ₀ — намагничивающую (почти постоянную) составляющую (I₀ ? I_1 м) и —^?₂ —переменную составляющую, компенсирующую МДС ротора.

Следовательно, ток ротора I₂ оказывает на магнитную систему двигателя такое же размагничивающее влияние, как и ток вторичной обмотки трансформатора (см. § 1.5). Таким образом, любое изменение механической нагрузки на валу двигателя сопровождается соответствующим изменением тока в обмотке статора I₁ так изменение этой нагрузки двигателя вызывает изменение скольжения s. Это, в свою очередь, влияет на ЭДС обмотки ротора [см.(12.6)], а следовательно, и на ток ротора I₂. Но так как этот ток развивает размагничивающее действие на магнитную систему двигателя, то его изменения вызывают соответствующие изменение тока в обмотке статора I₁ за счет составляющей — I^?₂. Так, в режиме холостого хода, когда нагрузка на валу двигателя отсутствует и s ? 0, ток I₂ ? 0. В этом случае ток в обмотке статора ₁ ?₀. Если же ротор двигателя затормозить, не отключая обмотку статopa от сети (режим короткого замыкания), то скольжение s = 1 и ЭДС обмотки ротора Е_2s достигает своего наибольшего значения Е₂. Также наибольшего значения достигнет ток I₂, а следовательно, и ток в обмотке статора I₁.

Приведение параметров обмотки ротора и векторная диаграмма асинхронного двигателя Чтобы векторы ЭДС, напряжений и токов обмоток статора и ротора можно было изобразить на одной векторной диаграмме, следует параметры обмотки ротора привести к обмотке статора, т. е. обмотку ротора с числом фаз m₂, обмоточным коэффициентом k_o62 и числом витков одной фазной обмотки щ₂ заменить обмоткой с m₁, щ₁ и k_об1. При этом мощности и фазовые сдвиги векторов ЭДС и токов ротора после приведения должны остаться такими же, что и до приведения. Пересчет реальных параметров обмотки ротора на приведенные выполняется по формулам, аналогичным формулам приведения параметров вторичной обмотки трансформатора (см. § 1.6).

При s = 1 приведенная ЭДС ротора.

E'2 = E2 ke, (12.17).

где k_e = E₁/ E₂ =k_o61 щ₁ /(k_o62/ щ₂) — коэффициент трансформации напряжения в асинхронной машине при неподвижном роторе. Приведенный ток ротора.

I^?₂ = I₂/ k_i, (12.18).

где k_i = m₁ щ₁ k_oб1/ (m₂ щ₂ k_o62) = m₁ k_e/ m₂ — коэффициент трансформации тока асинхронной машины.

В отличие от трансформаторов в асинхронных двигателях коэффициенты трансформации напряжения и тока не равны (k_е? k_i). Объясняется это тем, что число фаз в обмотках статора и ротора в общем случае не одинаково (m₁? m₂). Лишь в двигателях с фазным ротором, у которых m₁ = m₂, эти коэффициенты равны.

Активное и индуктивное приведенные сопротивления обмотки ротора:

r^?₂ = r₂ k_e k_i ;

x^?₂ = x₂ k_e k_i. (12.19).

Следует обратить внимание на некоторую специфику определения числа фаз m₂ и числа витков щ₂ для короткозамкнутой обмотки ротора (см. рис. 10.3). Каждый стержень этой обмотки рассматривают как одну фазу, а поэтому число витков одной фазы короткозамкнутой обмотки ротора щ₂ =, 0,5; обмоточный коэффициент такой обмотки k_об2 = 1, а число фаз m₂ = Z₂, т. е. равно числу стержней в короткозамкнутой обмотке ротора.

Подставив в (12.9) приведенные значения параметров обмотки ротора Е^?₂, I^?₂, r₂ и x^?₂, получим уравнение напряжений обмотки ротора в приведенном виде:

^?₂ — j^?₂ x^?₂ - ^?₂r^?₂/ s =0 (12.20).

Величину r?₂/ s можно представить в виде.

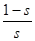
= - + r^?₂ = r^?₂ + r^?₂ (12.21).

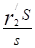
тогда уравнение ЭДС для цепи ротора в приведенных параметрах примет вид.

0 =^?₂ — j^?₂x₂ - ^?₂r^?₂ r^?₂(1-s)/ s. (12.22).

Для асинхронного двигателя (так же как и для трансформатора) можно построить векторную диаграмму. Основанием для построения этой диаграммы являются уравнение токов (12.14) и уравнения напряжений обмоток статора (12.3) и ротора.

Угол сдвига фаз между ЭДС ^?₂ и током ^?₂

Ш₂ = arctg (x^?₂s/ r^?₂).

Так как векторную диаграмму асинхронного двигателя строят по уравнениям напряжений и токов, аналогичным уравнениям трансформатора, то порядок построения этой диаграммы такой же, что и векторной диаграммы трансформатора (см. § 1.7).

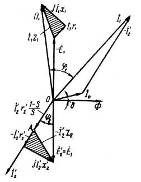
Рис. 12.1 Векторная диаграмма асинхронного двигателя

На рис. 12.1 представлена векторная диаграмма асинхронного двигателя. От векторной диаграммы трансформатора (см. рис. 1.19) она отличается тем, что сумма падений напряжения в обмотке ротора (во вторичной обмотке) уравновешивается ЭДС ^?₂ обмотки неподвижного ротора (n₂ = 0), так как обмотка ротора замкнутой накоротко. Однако если падение напряжения =^?₂r^?₂ (1-s)/ s рассматривать как напряжение на некоторой активной нагрузке r^?₂ (1-s)/ s, подключенной на зажимы неподвижного ротора, то векторную диаграмму асинхронного двигателя можно рассматривать как векторную диаграмму трансформатора, на зажимы вторичной обмотки которого подключено переменное активное сопротивление r₂ (1-s)/ s. Иначе говоря, асинхронный двигатель в электрическом отношении подобен трансформатору работающему на чисто активную нагрузку. Активная мощность вторичной обмотки такого трансформатора.

Р^?₂ = m₁ I^?₂² r^?₂(1-s)/s (12.23).

представляет собой полную механическую мощность, развиваемую асинхронным двигателем.

Уравнениям напряжений и токов, а также векторной диаграмме асинхронного двигателя соответствует электрическая схема замещения асинхронного двигателя.

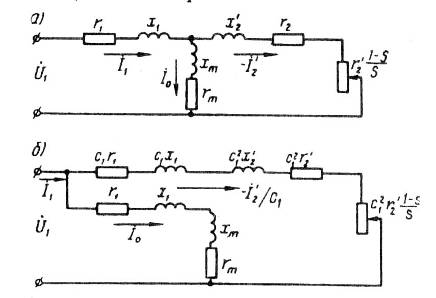
Рис. 12.2. Схемы замещения асинхронного

На рис. 12.2, а представлена Т-образная схема замещения. Магнитная связь обмоток статора и ротора в асинхронном двигателе на схеме замещения заменена электрической связью цепей статора и ротора. Активное сопротивление можно рассматривать как внешнее сопротивление, включенное в обмотку неподвижного ротора. В этом случае асинхронный двигатель аналогичен трансформатору, работающему на активную нагрузку. Сопротивлениеединственный переменный параметр схемы. Значение этого сопротивления определяется скольжением, а следовательно, механической нагрузкой на валу двигателя. Так, если нагрузочный момент на валу двигателя М₂ = 0, то скольжение s? 0. При этом r₂' (1 — s)/ s = ?, что соответствует работе двигателя в режиме х.х. Если же нагрузочный момент на валу двигателя превышает его вращающий момент, то ротор останавливается (s = 1). При этом r₂'(1 — s)/ s = О, что соответствует режиму к.з. асинхронного двигателя.

Более удобной для практического применения является Гобразная схема замещения (рис. 12.2, б), у которой намагничивающий контур (Z_m = r_m+ j x_m) вынесен на входные зажимы схемы замещения. Чтобы при этом намагничивающий ток I₀ не изменил своего значения, в этот контур последовательно включают сопротивления обмотки статора r₁ и х₁. Полученная таким образом схема удобна тем, что она состоит из двух параллельно соединенных контуров: намагничивающего с током ₀ и рабочего с током — ^?₂. Расчет параметров рабочего контура Г-образной схемы замещения требует уточнения, что достигается введением в расчетные формулы коэффициента с₁ (рис. 12.2, б), представляющего собой отношение напряжения сети U₁ к ЭДС статора Е₁ при идеальном холостом ходе (s = 0) [1]. Так как в этом режиме ток холостого хода асинхронного двигателя весьма мал, то U₁ оказывается лишь немногим больше, чем ЭДС Е₁, а их отношение с₁ =U₁/ E₁ мало отличается от единицы. Для двигателей мощностью 3 кВт и более с₁ = 1,05 ч 1,02, поэтому с целью облегчения анализа выражений, характеризующих свойства асинхронных двигателей и упрощения практических расчетов, примем с₁ = 1. Возникшие при этом неточности не превысят значений, допустимых при технических расчетах. Например, при расчете тока ротора I^?₂ эта ошибка составит от 2 до 5% (меньшие значения относятся к двигателям большей мощности).

Воспользовавшись Г-образной схемой замещения и приняв с₁ = 1, запишем выражение тока в рабочем контуре:

I^?₂ = (12.24).

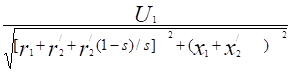
или с учетом (12.21) получим.

I^?₂ =. (12.25).

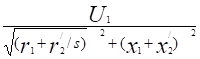
Знаменатель выражения (12.25) представляет собой полное сопротивление рабочего контура Г-образной схемы замещения. асинхронного двигателя.