Метод трапеций. 
Приближенные методы вычисления определенных интегралов

Разобьем отрезок на равных частей при помощи точек:

, , .

Метод трапеций заключается в замене интеграла суммой:

.

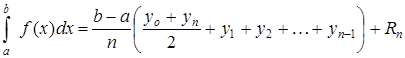
Для приближенных практических расчетов применяется формула:

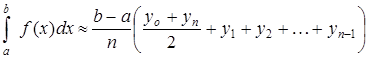
. (3).

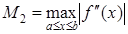
Абсолютная погрешность приближения, полученного по формуле трапеций, оценивается с помощью формулы, где .

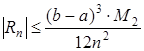
Метод парабол (метод Симпсона)

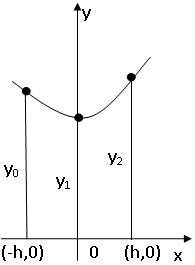
а) Через любые три точки с координатами проходит только одна парабола .

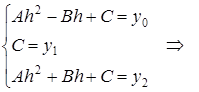
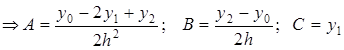
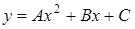
б) Выразим площадь под параболой на отрезке через :

.

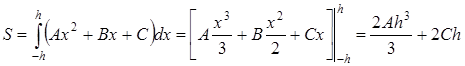
Учитывая значения и из пункта а) следует:

.

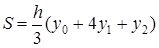
в) Разобьем отрезок на равных частей при помощи точек:

, , .

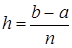
Метод парабол заключается в замене интеграла суммой:

.

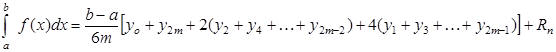
Для приближенных практических расчетов применяется формула:

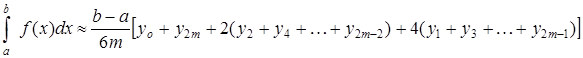
. (4).

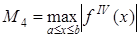
Абсолютная погрешность вычисления по формуле (4) оценивается соотношением, где .

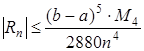
Оценка точности вычисления «неберущихся» интегралов

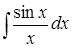
В данной работе вычисление абсолютной и относительной погрешности проводится при условии, что известно точное значение определенного интеграла. Однако не всякая первообразная, даже тогда, когда она существует, выражается в конечном виде через элементарные функции. Таковы первообразные, выраженные интегралами, ,, и т. д. Во всех подобных случаях первообразная представляет собой некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций.

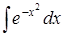
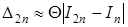
Определенные интегралы от таких функций можно вычислить только приближенно. Для оценки точности вычисления в таких случаях используют, например, правило Рунге. В данном случае интеграл вычисляется по выбранной формуле (прямоугольников, трапеций, парабол Симпсона) при числе шагов, равном n, а затем при числе шагов, равном. Погрешность вычисления значения интеграла при числе шагов, равном, вычисляется по формуле Рунге, для формул прямоугольников и трапеций, а для формулы Сипсона. Таким образом, интеграл вычисляется для последовательных значений числа шагов, , …, где — начальное число шагов. Процесс вычислений заканчивается, когда для очередного значения будет выполнено условие, где — заданная точность.

Для того чтобы не вычислять один и тот же интеграл по нескольку раз для разных разбиений отрезка интегрирования, можно вычислить шаг интегрирования заранее.

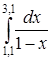
Пример. Выбрать шаг интегрирования для вычисления интеграла с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона.

Квадратурная формула прямоугольников.

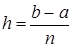
Вычислим, при каком шаге погрешность будет составлять 0,01:

подынтегральный трапеция парабола неберущийся.

.

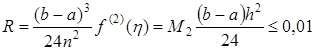
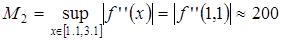
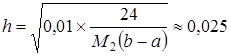
Поскольку, то .

При шаге отрезок разбивается на равностоящих узлов.

Квадратурная формула трапеций.

Вычислим, при каком шаге погрешность составит 0,01:

.

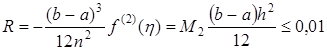
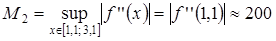
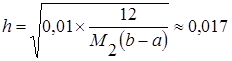
Поскольку, .

При шаге, отрезок разбивается на равностоящих узлов.

Квадратурная формула Симпсона.

Вычислим, при каком шаге погрешность составит 0,01:

.

.

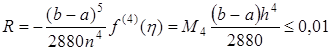
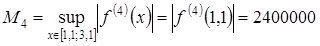
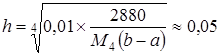
При шаге, отрезок разбивается на равностоящих узлов.

Как и следовало ожидать, наименьшее количество равностоящих узлов получается при вычислении интеграла по квадратурной формуле Симпсона.

Содержание РГР «Приближенные методы вычисления определенных интегралов».

Студенту предлагается работа, состоящая из четырех этапов:

• 1 этап — точное вычисление определенного интеграла.
• 2 этап — приближенное вычисление определенного интеграла одним из методов: прямоугольников или трапеций.
• 3 этап — приближенное вычисление определенного интеграла методом парабол.

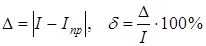
4 этап — расчет и сравнение абсолютной и относительной ошибок приближенных методов:, где — точное решение интеграла, — значение интеграла, полученное с помощью приближенных методов.

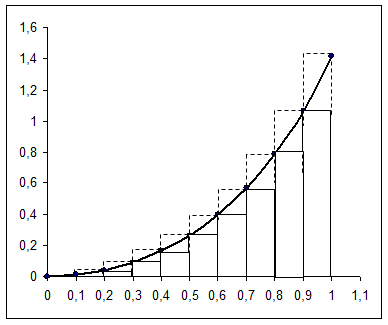
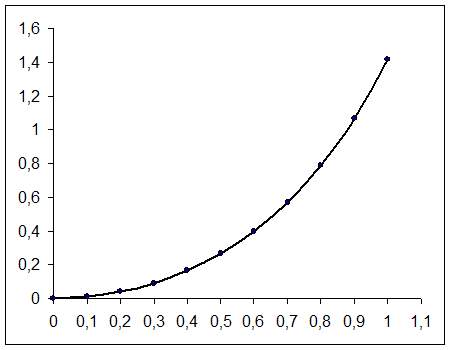
Построение графика подынтегральной функции.

Варианты и образец выполнения РГР приведены ниже.

Варианты.

№ варианта.	f (x).	a.	b.	Шаг h.
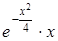			0,1.
			0,1.
			0,1.
			0,1.
		р	0,1р
			0,1.
			0,1.
			0,1.
			0,1.
		р/2.	0,05р
			0,1.
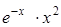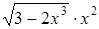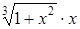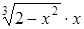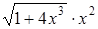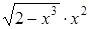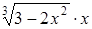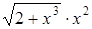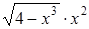			0,1.
			0,1.
			0,1.
		р	0,1р
			0,1.
			0,1.
		р/2.	0,05р
			0,1.
		р/2.	0,05р
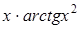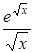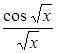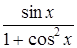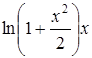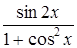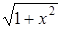			0,1.
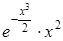			0,1.
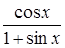		р/2.	0,05р
		р/2.	0,05р
		р/2.	0,05р
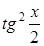		р/2.	0,05р
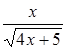			0,1.
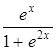			0,1.
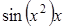		р/2.	0,05р
			0,1.

Образец выполнения РГР Задание. Вычислить интеграл.

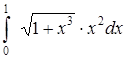
1. Точное вычисление:

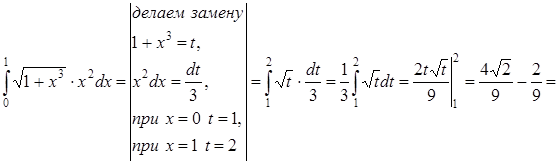
= 0,40 631 714.

2. Приближенное вычисление с помощью формул прямоугольников:

.

.

.

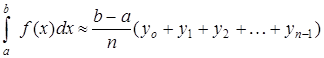
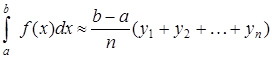
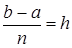
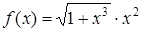
Составим таблицу:

№.	xi.	yi = f (xi).
	0,1.	0,10 005.
	0,2.	0,4 016.
	0,3.	0,91 207.
	0,4.	0,165 041.
	0,5.	0,265 165.
	0,6.	0,396 981.
	0,7.	0,567 851.
	0,8.	0,786 966.
	0,9.	1,65 081.
		1,414 214.

По первой формуле прямоугольников получаем:

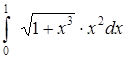
? 0,1 = 0,1· 3,62 514 = 0,306 251.

По второй формуле прямоугольников получаем:

? 0,1 = 0,1· 4,802 669 = 0,480 267.

В данном случае первая формула дает значение интеграла с недостатком, вторая — с избытком.

Вычислим относительную и абсолютную погрешности.

I = 0,40 631 714, ,.

.

.

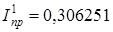
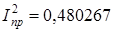
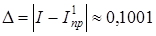
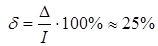
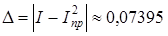
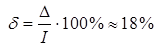
3. Приближенное вычисление по формуле трапеций:

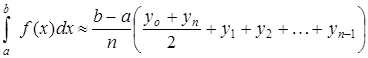
В нашем случае получаем:

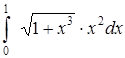
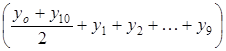
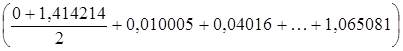
? 0,1 = =0,1 = 0,1· 4,95 562 = =0,409 556.

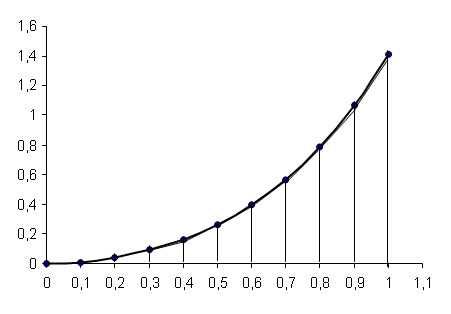
Вычислим относительную и абсолютную погрешности.

I = 0,40 631 714,.

.

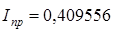
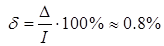
4. Приближенное вычисление по формуле Симпсона:

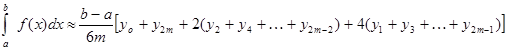
В нашем случае получаем:

? =.

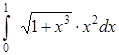
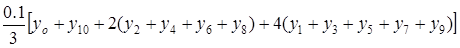
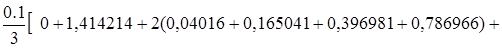
= = 0,406 325.

Вычислим относительную и абсолютную погрешности.

I = 0,40 631 714.

.

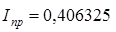
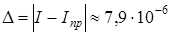
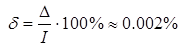
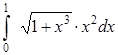
В действительности, = 0,40 631 714.

Таким образом, при разбиении отрезка на 10 частей по формуле Симпсона мы получили 5 верных знаков; по формуле трапеций — три верных знака; по формуле прямоугольников мы можем ручаться только за первый знак.