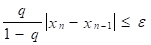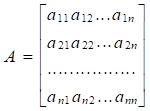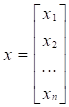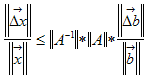Другие работы

Возьмем для примера газовые гидраты, в которых роль «хозяина» выполняет вода, а «гостями» могут быть молекулы одного из таких веществ, как ксенон, метан, пропан, сернистый газ, сероводород, хлор и т. д. Разнообразие «гостей» вызвано особенностью молекул «хозяина», т. е. воды. Обычная вода при замерзании образует кристаллы льда, который имеет при разных давлениях множество модификаций. Связано это…
Реферат 
Стандартные электродные потенциачы Е° — количественные характеристики систем, состоящих из металла и гидратированных катионов в водном растворе. Электрод Li*(p)/Li (i<) обладает самым большим отрицательным потенциалом, поэтому металлический литий будет самым сильным восстановителем, если в результате реакции образуются гидратированные катионы Li+. Электрод Аи3+(р)/Аи (к) имеет самый большой…
Реферат 
В чем заключается необходимость выработки особых этических требований к деятельности ученого? Назовите эти требования. Что такое культура? Что общего и в чем различия между естественно-научной и гуманитарной культурами? Где и почему наиболее тесно переплетаются философские и естественно-научные знания? Обоснуйте это. Какое различие существует между фундаментальными и прикладными науками? Как они…
Реферат 
В силу хорошей растворимости многих солей большая часть земной воды является соленой. Только 0,6% жидкой воды гидросферы является доступной пресной водой, пригодной для питья. Активность воды как растворителя приводит к тому, что в чистом виде вода — это специальный химический реактив, очень чувствительный к условиям хранения. Понимание химического аспекта опасности для окружающей среды нарушения…
Реферат 
Расчет pH до точки эквивалентности. 1. После начала титрования в растворе образуется соль слабого основания и сильной кислоты — Ш4С1: Рассчитаем значения pH в различные моменты титрования 10 мл 0,1 н. раствора аммиака 0,1 н. раствором хлороводородной кислоты. Рассчитаем значение pH в момент титрования, когда добавлено 9,99 мл 0,1 н. раствора НС1: с0 = 0,0001 моль/л; с (соли) = 0,0999 моль/л…
Реферат 
Так как «рост» частиц протекает при возрастании температуры и, соответственно, увеличении скорости их движения, то для каждой частицы существует определённый температурный и скоростной порог их формирования. Такие частицы закончат свой «рост» и увеличение массы при достижении ими скорост света и максимального температурного порога, равного ~1013 К. Такой образовавшейся частицей и будет нейтрон…
Реферат 
Методология исследования охватывает как перекрёстную выборку, так и анализ панельных данных, с помощью которых вычислены параметры устойчивости и. В первом случае значения составляют 0.62 и 0.56, а во втором — 0.57 и 0.65 соответственно. Авторы статьи сравнивают способность оригинальной модели Ольсона и спецификации, скорректированной на величину инфляции, прогнозировать анормальную прибыль на 1…
Реферат 
В соответствии с законодательством о труде каждый работник имеет право на рабочее место, соответствующее требованиям охраны труда, и компенсации по условиям труда, установленные законодательством. Наниматель обязан обеспечить безопасность работников и защиту от рисков всех лиц, находящихся в непосредственной близости от рабочих мест или мест производства работ. При выполнении работ над водой…
Реферат 
Для защиты цехового трансформатора при однофазных КЗ в обмотке и на выводах НН, а также в сети НН принимаем МТЗ нулевой последовательности c выдержкой времени с использованием реле РТ -40. защиту выполняем с помощью одного токового реле, включенного на ТТ, установленной в цепи заземления нейтрали цехового трансформатора. В реле протекает полный ток однофазного КЗ. Приведенная формула справедлива…
Реферат 
А REF рис38 h 3.8J (цифрами обозначены: 1 — J =6,2*10−4,8; 2 — J =6,2*10−5; 3 — J =6,2*10−6;). Динамика изменения угловой скорости при варьировании параметра J соответствует динамике изменения угла поворота, в связи с чем здесь не приводится. Из эксперимента видно, что увеличение момента инерции J приводит к уменьшению времени переходного процесса, что соответствует использованной модели, так…
Реферат 
Предположим теперь, что строго вдоль меридиана проложен стеклянный стержень длиной L, внутри которого со скоростью u движутся световые импульсы, как это было в эксперименте Шамира и Фокса. Как и в движущейся системе координат в неподвижной системе световые импульсы движутся строго вдоль стеклянного стержня, однако сам стеклянный стержень смещается с орбитальной скоростью перпендикулярно…
Реферат 
N=1С Для определения количества пределов измерения омметра воспользуемся формулой (1.12). R2 = 17.106 Ом По формуле (1.4) определим сопротивление регулятора «бесконечности» R1. R6 = 0.362 Ом По формуле (1.9) определим максимальное значение силы тока омметра. Е0= 12 В По формуле (1.2) определим добавочное сопротивление R2. Схема омметра основана на совмещении схем рис 1.2 и 1.3. Полученная схема…
Реферат 
Число установленных на проектируемой подстанции главных понижающих трансформатора. Сопротивление системы до шин районных подстанций РП1 и РП2 определяем по формуле. Таблица 6.1. Расчет токов, мощностей и теплового импульса КЗ в точках К1, К2. Рассчитываем эквивалентные сопротивления до точек короткого замыкания. Узловые — присоединяемые к сети не менее чем тремя питающими линиями. Сопротивление…
Реферат 
Тяговые подстанции расставить на электрифицированном участке можно после определения количества опорных и промежуточных подстанций. На участках, электрифицированных на переменном токе, опорные подстанции сооружаются не реже, чем через 3 промежуточные. Рисунок 2.1 Условное подключение тяговых подстанций Количество районов контактной сети (ЭЧК) устанавливается исходя из эксплуатационной длины…
Реферат 
Элементарными частицами называют мельчайшие неделимые частицы вещества, которые не имеют внутренней структуры или, точнее, она еще не известна. Элементарные частицы могут вступать в реакции с другими частицами, при этом возникают новые частицы. Например, реакции взаимопревращения нейтрона и протона происходит с возникновением электрона, позитрона, нейтрино н, антинейтрино н~. Кроме электронов…
Реферат