Эйлеров путь и Эйлеров цикл на графе

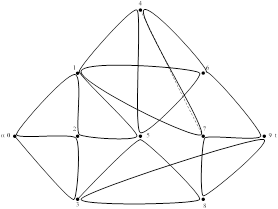
Для определения Эйлерова путь требуется выписать степенную последовательность вершин графа G и указать в графе G Эйлеров путь.

Если такового пути не существует, то в графе G добавить наименьшее число ребер таким образом, чтобы в новом графе можно было указать Эйлерову цепь.

Степенная последовательность вершин графа G:

(3,6,4,5,3,6,4,3,4,4).

Для существования Эйлерова пути допустимо только две вершины с нечетными степенями, поэтому необходимо добавить одно ребро, скажем между вершинами 4 и 7.

Полученный Эйлеров путь: 0,3,2,0,1,2,5,1,4,5,6,1,7,4,6,9,7,8,9,3,8,5,3.

Схема Эйлерова пути приведена на рис. 1.4 (добавленное ребро показано пунктиром):

Рисунок 1.4 — Эйлеров путь, полученный путем добавления ребра.

Эйлеров цикл

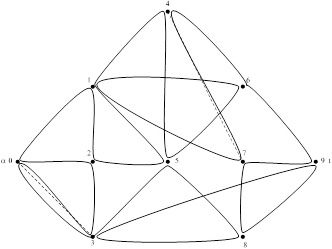
Эйлеров цикл позволяет обойти граф, проходя по каждому ребру только один раз. Незадействованных ребер быть не должно. Если такого цикла не существует, то в графе G добавить наименьшее число ребер таким образом, чтобы в новом графе можно было указать Эйлеров цикл.

Аналогично пункту 1.4.1 добавляем ребро {3,0}, замыкая Эйлерову цепь (при этом выполняя условие существования Эйлерова цикла — четность степеней всех вершин). Ребро {3,0} кратное, что не противоречит заданию, но при необходимости можно ввести ребра {0,7} и {4,3} вместо ранее введенных. Полученный Эйлеров цикл: 0,3,2,0,1,2,5,1,4,5,6,1,7,4,6,9,7,8,9,3,8,5,3,0. Схема Эйлерова цикла (добавленные ребра показаны пунктиром):

Рисунок 1.5 — добавление двух ребер для получения Эйлерова цикла.