Прогнозирование объемов перевозок авиакомпании

Цель прогнозирования — определение наиболее устойчивых закономерностей и тенденций, предсказание на их основе показателей в будущем. Прогнозирование основано на информации о предшествующем состоянии системы, тенденциях и взаимосвязях, обнаруживших себя в прошлом.

Основной элемент прогнозирования — экономико-математическое моделирование с помощью современной вычислительной техники. Прогнозирование основано на информации о предшествующем состоянии экономической системы, на тенденциях и взаимосвязях, обнаруживавших себя в прошлом.

Линейная зависимость выражается формулой:

y_t ^' = а + b t, (1).

где y_t — выравненное значение, соответствующее моменту времени; и — константы, которые обращают сумму квадратов отклонений фактических значений y_t от выравненных y_t в минимум. Параметры a и b, обращающие сумму квадратов (y_t — y_t)² в минимум, вычисляются по формуле:

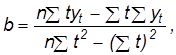
(2).

где b называют коэффициентом регрессии; он характеризует наклон линии регрессии, знак здесь и далее означает суммирование .

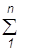
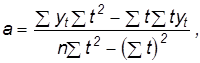
(3).

Коэффициент а называют начальным или свободным коэффициентом. Он характеризует уровень пересечения линии регрессии с осью ординат y, т. е. равен y_tпри t = 0.

Для того чтобы найти прогноз, необходимо оценить сначала параметры линейного тренда, подставить их в исходное уравнение кривой, а затем вычислить прогноз.

Метод наименьших квадратов и процедура подбора прямой регрессии полностью переносятся и на случай, когда уравнение кривой может быть после некоторых преобразований сведено к линейному тренду.

В практике криволинейного выравнивания широко распространены два вида преобразований: натуральный логарифм (ln) и обратное преобразование (1/t). При этом, очевидно, возможно преобразование как зависимой переменной y, так и независимой t или одновременно и той, и другой. В таблице 6 представлены восемь возможных преобразований кривых, полученных на основе логарифмирования и обратного преобразования.

Таблица 6.

Кривые, сводящиеся к уравнению прямой преобразованием исходных данных.

При выборе наилучшей кривой для прогнозирования используют средний квадрат ошибки (MSE), среднеабсолютную процентную ошибку (MAPE), коэффициент детерминации (r).

Коэффициент детерминации можно определить с помощью уравнения:

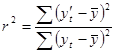
(4).

где .

Средний квадрат ошибки (MSE) определяется формулой:

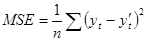
. (5).

Среднеабсолютная процентная ошибка (MAPE) есть среднее абсолютных значений ошибок прогноза, выраженных в % относительно фактических значений показателя у_t

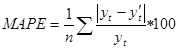
. (6).

Типичные значения MAPE и их интерпретация показаны в таблице 7.

Таблица 7.

Интерпретация типичных значений MAPE.

• 1. По данным динамического ряда (таблица 2) были рассчитаны параметры а, b аппроксимирующих зависимостей согласно таблице 6.
• 2. Построим графики изменения выполненного общего тонно-километража авиакомпании за 10 лет для каждой из аппроксимирующих зависимостей.

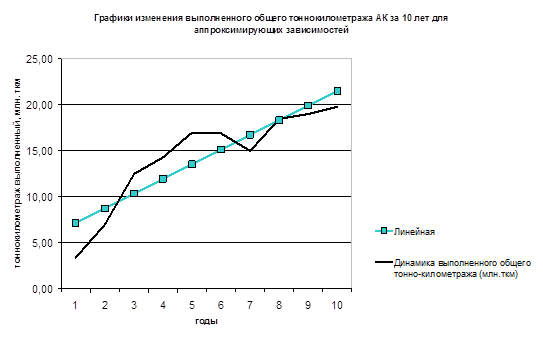
График № 1.

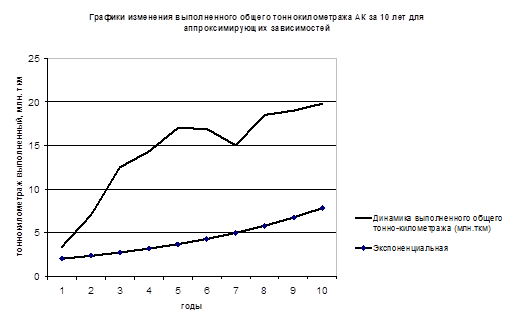
График № 2.

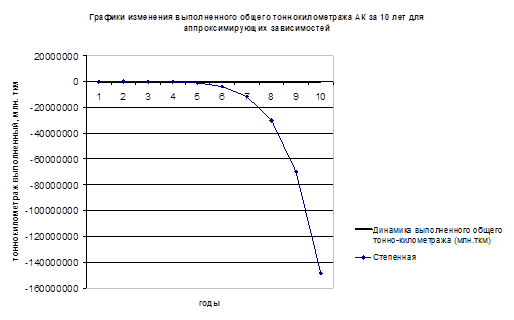
График № 3.

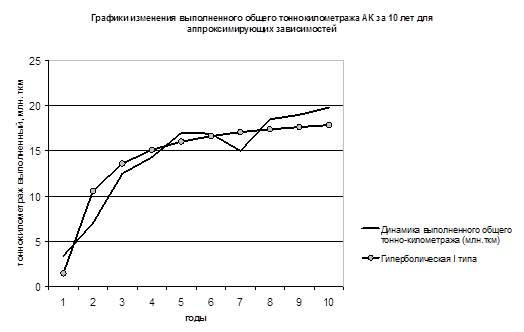
График № 4.

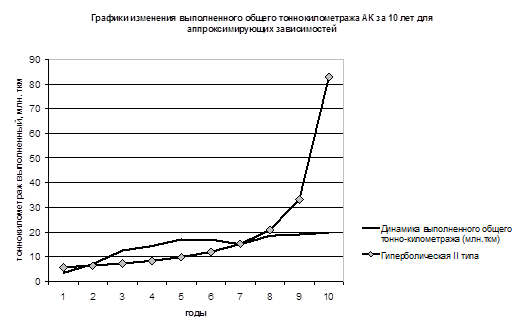
График № 5.

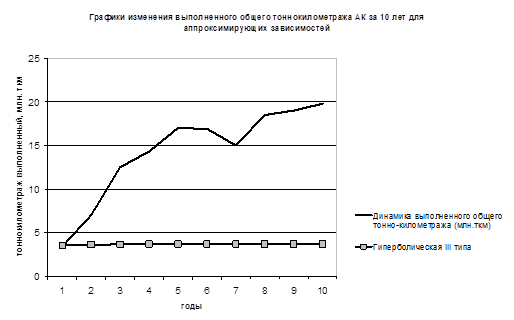
График № 6.

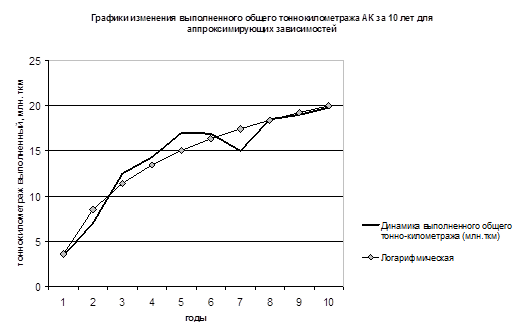
График № 7.

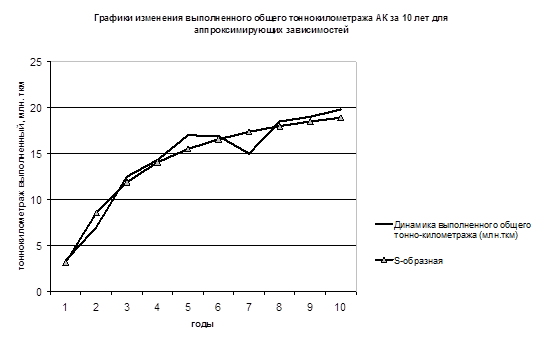
График № 8.

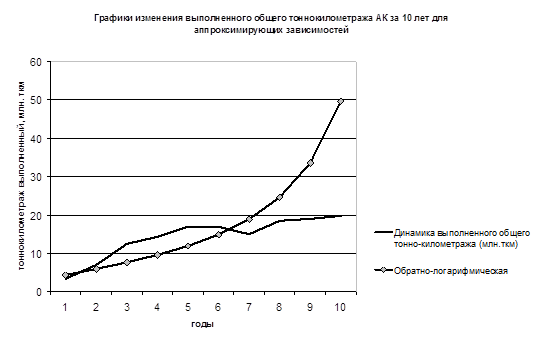
График № 9.

3. Рассчитаны показатели r, MSE, MAPE для каждой из аппроксимирующих зависимостей. Результаты расчетов представлены в виде таблицы 8.

Таблица 8.

Результаты аппроксимации.

4. Из полученных расчетов видно, что с наиболее высокой точностью (значение среднеабсолютной ошибки составило 7,18%) тенденции изменения объемов тоннокилометража авиакомпании показывает S-образная зависимость, описываемая уравнением yt = e3,14−1,98/t. Поэтому применим ее для прогнозирования общего тонно-километража АК на 11-й год.

И в результате расчета можно сказать, что с вероятностью 92,82% общий выполненный тонно-километраж по итогам 11 года составит 19,25 млн.ткм.