Механическая характеристика рабочей машины

Механической характеристикой рабочей машины называется зависимость приведенной к валу двигателя угловой скорости от момента сопротивления w=f (М_с).

При поступательном движении соответственно — линейная скорость в функции усилия V=f (F_c).

М_с — статический момент, складывается из момента на трение (пропорциональна весу вращающихся частей и диаметру опоры), момента от трения на рассекание воздуха (возрастающая функция от частоты вращения), собственно полезный М_с (от типа рода нагрузки).

По характеру действия моменты нагрузки М_с делятся на активные и реактивные:

Активные — имеют постоянное, не зависящие от скорости, направление своего действия и создаются так называемыми потенциальными силами — силами притяжения Земли, силами упругой деформации и др.

Реактивные — создаются в основном силами трения, они всегда противодействуют движению и поэтому изменяют свой знак с изменением направления скорости движения.

Различные производственные механизмы обладают различными механическими характеристиками которые можно описать выражением М_с=М₀+(М_с.н -М₀)()^x, (1).

где М_с — момент сопротивления производственного механизма (рабочей машины) при скорости w (текущей скорости);

М_с.н — номинальный момент сопротивления при w_н;

М₀ — начальный момент сопротивления при w=0;

w — текущая угловая скорость;

х — показатель степени, характеризующий изменение момента сопротивления при изменении скорости.

Приведенная, формула позволяет классифицировать механические характеристики производственных механизмов, ориентировочно, на следующие основные категории (рис.1).

• 1- не зависящая от скорости характеристика, х=0
• (подъемные краны, лебедки, механизмы подачи металлорежущих станков, поршневые насосы при неизменной высоте подачи, конвейеры, транспортеры с постоянной нагрузкой). Сюда же могут быть отнесены все механизмы, у которых основным моментом сопротивления является момент трения, т.к. обычно в пределах рабочих скоростей момент трения изменяется мало;
• 2- линейно возрастающая, х=1
• (генераторы постоянного тока с независимым возбуждением работающий на постоянную внешнюю нагрузку, зерноочистительные машины);
• 3- нелинейно-возрастающая, х=2 — называют вентиляторной характеристикой (вентиляторы, центрифуги, сепараторы, центробежные насосы);
• 4- нелинейно-спадающая, х= -1 (токарные, расточные, фрезерные и другие металлорежущие станки, зерновые нории).

Эти характеристики не исчерпывают всех практических возможных случаев, но дают представление о типичных производственных механизмах.

Целесообразно установить зависимость мощности от скорости для каждой группы механизмов.

Если пренебречь М₀ в выражении (1), уравнение примет вид М_C= М_C.Н ^. ()^Х; (2).

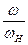
умножим правую и левую части на w, получим Р_С =М_С ^. w = М_С.Н ^. ()^{X .} w = М_С.Н ^., (3).

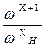
где Р_С — мощность потребляемая механизмом при скорости w.

При х=0 Р_С1 =М_С.Н ^. w= К₁ w; х=1 Р_С2 = w²= К₂ w²;

х=2 РС3 = w3= К3 w3; х= -1 РС4 =МС.Н. wн= const.

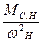
Таким образом, для механизмов первой группы мощность пропорционально скорости, для механизмов второй — квадрату скорости, третьей — кубу скорости, четвертой — не зависит от скорости.