Типовой расчет по теории вероятностей

Если верна вторая гипотеза — из первой урны переложили черный шар, то во второй урне есть 4 черных шара и 1 белый. Если верна вторая гипотеза — из первой урны переложили черный шар, то во второй урне есть 4 черных шара и 1 белый. Если верна первая гипотеза — из первой урны переложили белый шар, то во второй урне есть 3 черных шара и 2 белых. Если верна первая гипотеза — из первой урны переложили… Читать ещё >
Типовой расчет по теории вероятностей (реферат, курсовая, диплом, контрольная)
Задача 1.
Студенты выполняют экзаменационную работу в классе контролирующих машин. Работа состоит из трех задач. Для получения положительной оценки достаточно решить две. Для каждой задачи зашифровано пять ответов, из которых только один правильный. Студент N плохо знает материал и поэтому выбирает ответы для каждой задачи наудачу. Какова вероятность того, что он получит положительную оценку?
Решение:

P (A) = - классическая конструкция вероятности.
m — число благоприятных исходов этого события;
n — общее число всех возможных исходов этого события.
А =.
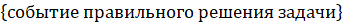
В =.
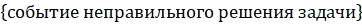
Вероятность правильного решения задачи: P (A) =.
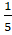
Вероятность неправильного решения задачи: P (В) =.
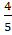
Получить положительную оценку можно дав 2 либо же 3 правильных ответа. Вероятность получить 3 правильных ответа:
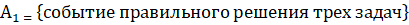
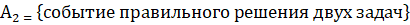
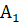
P () = P (A)*P (А)*P (А) — теорема умножения независимых событий.
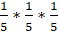
P () = = 0,008.
Вероятность получить 2 правильных ответа:
Студент N может получить правильный ответ в 1 и 2 задаче, или в 1 и 3, или 2 и 3, а это три варианта!
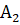
P () = P (A)*P (А)*P (В)*3.
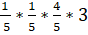
P () = = 0,096.
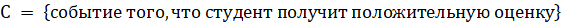
Р © = P ()+ P ().
Р © = 0,008 + 0,096 = 0,104.
вероятность того, что студент получит положительную оценку.
Ответ: 0,104.
Задача 2.
Первая урна содержит 3 красных, 2 белых и 1 синий шар. Вторая урна содержит 4 белых и 2 синих шара. Бросается игральная кость. Если на ней выпало 1 или 6 очков, вынимается шар из первой урны, в противном случае из второй. Вытащен синий шар.
Какова вероятность, что он взят из второй урны?
Решение:
Классическая конструкция вероятности.
P (A) =.
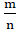
m — число благоприятных исходов этого события;
n — общее число всех возможных исходов этого события Обозначим через, А событие того, что вытащен синий шар.
Можно сделать два предположения:
- 1) Вытащен синий шар из первой урны (гипотеза В1)
- 2) Вытащен синий шар из второй урны (гипотеза В2)
Искомую вероятность того, что синий шар вытащен из второй урны, найдем по формуле Байеся:
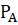
(B2) =.
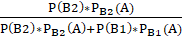
По условию задачи имеем:
P (B1) =.

вероятность того, что шар вытащен из первой урны (выпало 1 или 6 очков).
P (B2) =.

вероятность того, что шар вытащен из второй урны (выпало 2,3,4 или 5 очков).
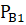
(А) =.

вероятность того, что вытащенный из первой урны шар синий).
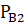
(А) =.
вероятность того, что вытащенный из второй урны шар синий) Искомая вероятность:
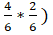
(B2) = (/ () = 0, 8.
Ответ: 0,8.
Задача 3.
Караван из 4 судов пересекает минное поле, вероятность подрыва для каждого из судов считается равной 0,1.
Найти вероятность того, что не менее половины судов уцелеет.
Решение:
P = 0,1 — вероятность подрыва для одного судна.
Q = 1- 0,1 = 0,9 — вероятность того, что одно судно уцелеет не взорвется.
А =.
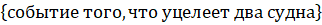
(А) =.
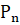
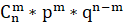
вероятность того, что уцелеет два судна по формуле Бернулли.
n = 4, m = 2:
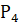
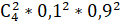
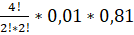
(А) = = = 0, 049.
=.
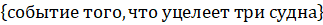
вероятность того, что уцелеет три судна по формуле Бернулли.
() =.
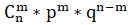
— вероятность того, что уцелеет четыре судна по формуле Бернулли.
n = 4, m = 3:
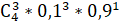
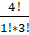
() = = *0,001*0,9 = 0,0036.
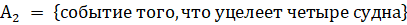
() =.
вероятность того,.
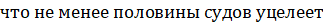
n = 4, m = 4:
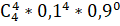
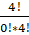
() = = *0,0001*1 = 0,0001.
С =.
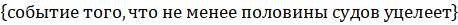
Р© = (А)+ ()+ () = 0,049+ 0,0036+ 0,0001 = 0,0527-.
Ответ: 0, 0527.
Задача 4.
Из урны, в которой было 4 белых и 2 черных шара, переложен один шар в другую урну, в которой находилось 3 черных шара и один белый. После перемешивания из последней урны вынимают 3 шара.
Построить *… отклонение числа черных шаров, вынутых из второй урны.
Найти вероятность того, что из нее будет извлечено:
- а) по крайней мере, два черных шара;
- б) не более двух черных шаров.
Решение:
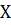
Случайная величина — число черных шаров, вынутых из второй урны, может принимать значения.
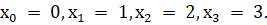
Гипотезы:
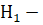
из первой урны вытащен белый шар;
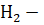
из второй урны вытащен черный шар;
Вероятности гипотез (по классическому определению вероятностей):
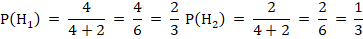
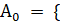
среди трех шаров, вынутых из второй урны, черных нет (вытянуты три белых шара}.
Условные вероятности (по классическому определению вероятностей):
1) Если верна первая гипотеза — из первой урны переложили белый шар, то во второй урне есть 3 черных шара и 2 белых.
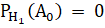
2) Если верна вторая гипотеза — из первой урны переложили черный шар, то во второй урне есть 4 черных шара и 1 белый.
Вероятность события по формуле полной вероятности равна:
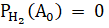
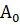
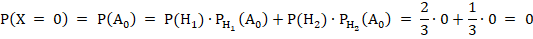
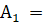
{среди трех шаров, вынутых из второй урны, есть один черный шар (и соответственно два белых шара}.
Условные вероятности (по классическому определению вероятностей):
1) Если верна первая гипотеза — из первой урны переложили белый шар, то во второй урне есть 3 черных шара и 2 белых.
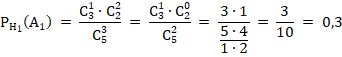
2) Если верна вторая гипотеза — из первой урны переложили черный шар, то во второй урне есть 4 черных шара и 1 белый.
Вероятность события по формуле полной вероятности равна:
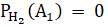
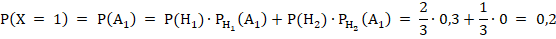
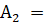
{среди трех шаров, вынутых из второй урны, есть два черных шара (и соответственно один белый шар}.
Условные вероятности (по классическому определению вероятностей):
1) Если верна первая гипотеза — из первой урны переложили белый шар, то во второй урне есть 3 черных шара и 2 белых.
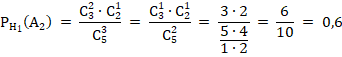
2) Если верна вторая гипотеза — из первой урны переложили черный шар, то во второй урне есть 4 черных шара и 1 белый.
Вероятность события по формуле полной вероятности равна:
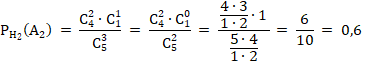
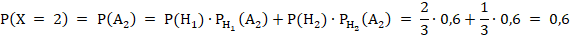
среди трех шаров, вынутых из второй урны, все три черных шара (и соответственно нет белых шаров}.
Условные вероятности (по классическому определению вероятностей):
1) Если верна первая гипотеза — из первой урны переложили белый шар, то во второй урне есть 3 черных шара и 2 белых.
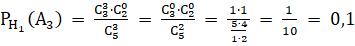
2) Если верна вторая гипотеза — из первой урны переложили черный шар, то во второй урне есть 4 черных шара и 1 белый.
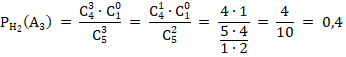
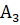
Вероятность события по формуле полной вероятности равна:
вероятность отклонение распределение ковариация регрессия.
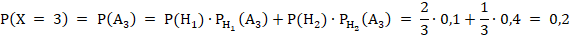
Закон распределения имеет вид:
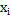 | |||
0,2. | 0,6. | 0,2. |
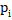
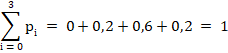
Функция распределения выглядит следующим образом.
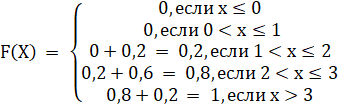
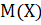
Математическое ожидание равно:
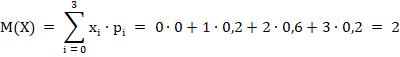
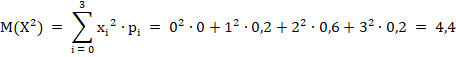
Дисперсия равна:
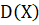
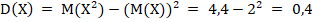
Среднее квадратическое отклонение равно.
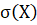
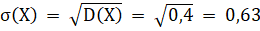
Найдем вероятность того, что из второй урны будет извлечено:
а) по крайней мере, два черных шара;
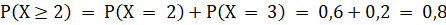
б) не более двух черных шаров.
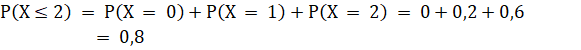
Задача 5.
Плотность распределения случайной величины X имеет вид.
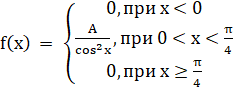
Найти:
- а) коэффициент А;
- б) функцию распределения F (x);
- в) математическое ожидание E (x);
- г) вероятность P ().
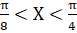
Решение:
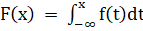
.
a) Значение постоянной A определяем из свойства плотности распределения:
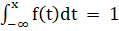
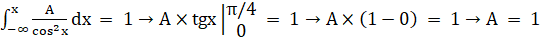
б) При x.
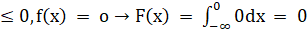
При 0tgx.
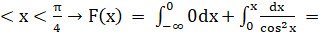
При x.
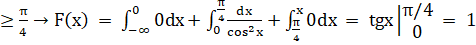
Таким образом, функция распределения F (x) имеет вид:
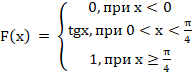
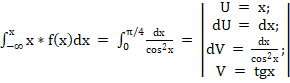
в) E (X) = = (x* tgx) ;
= =.
г) Найти вероятность того, что непрерывная случайная величина X примет значение из интервала ().
Воспользуемся формулой: P () =.
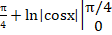
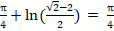
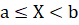
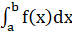
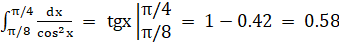
Задача 6.
Плотность распределения случайной величины X имеет вид:
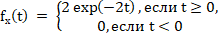
Случайные величины Y = exp (-2X) и Z = -4X-3 являются функциями от случайной величины X.
Найти: а) функцию распределения случайной величины Y;
б) моменты E (Z), D (Z), K (X, Z).
Решение:
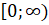
а) X распределена на, поэтому случайная величина Y = exp (-2X) распределена на.
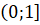
Если X = 0; Y = 1.
Если X.
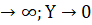
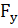
(a) = P (Y 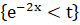
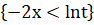
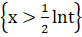

Нижний предел интегрирования должен быть положителен, и это выполняется при заданном интервале:
at (0;1).
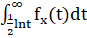
F ()) = ;
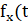
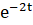
Для вычисления находим разность в т. — и, получаем:
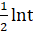
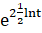
(t) = - = t,.
функция распределена равномерно.
б).
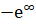
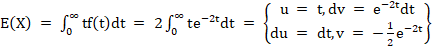
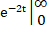
= t+dt =.
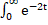
E (Z) = E (-4X-5) = -4−5 = -7.

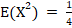
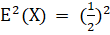
D (X) = — = 0.

D (Z) = D (-4X-5) = 0.
K (X, Z) =.
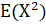
Типовой расчет по математической статистике.