Скоростная схема Верле

Одной из схем, обеспечивающей сохранение полной энергии (в смысле среднего), является скоростная схема Верле, которая и будет использована в данной работе. Это схема второго порядка точности, один шаг по времени в которой выполняется следующим образом:

1) из известных на начало шага данных (,, где — номер частицы, а — номер шага) рассчитываются скорости частиц на полушаге:

.

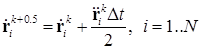
где — шаг численного интегрирования;

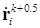
2) используя известные на начало шага и вычисленные находятся радиус-векторы :

;

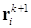
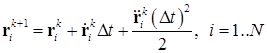
3) полученные ранее данные подставляются в исходную систему уравнений, откуда вычисляются ускорения частиц в конце шага:

;

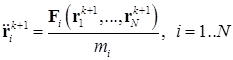
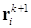
4) используя полученные ускорения находятся скорости в конце шага:

.

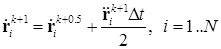
Проверим скоростную схему Верле, используя ее для решения задач, которые можно решить аналитически.

1) Решение задачи Коши для обыкновенного дифференциального уравнения.

Рассмотрим случай движения тела, на которое действует только сила трения.

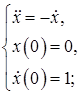
Решая данное уравнение относительно получим.

.

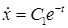
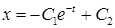
что с учетом начальных условий дает нам результат.

.

В силу того, что погрешность численного решения слишком мала, чтобы заметить ее на графике решения, приведем график модуля погрешности.

Погрешность мала и не возрастает больше определенного значения.

2) Параметрический резонанс.

В качестве более сложного теста рассмотрим уравнение.

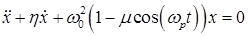
(26).

и, решая его численно, найдем первые две зоны параметрического резонанса.

Кратко опишем способ построения данных областей:

а) Задается фиксированное значение, в данном случае оно было равно .

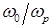
b) Для начального значения численно решается уравнение (26) при различных значениях отношения. Точки, в которых наблюдается параметрический резонанс, отмечаются на графике. Так получается одна горизонтальная линия на приведенном графике.

c) Значение изменяется, и находится следующая линия из зоны параметрического резонанса.

Вывод о том, наблюдается ли при данных значениях, и параметрический резонанс, делается путем сравнения амплитуды колебаний в начале и в конце — если амплитуда возросла в 40 раз, то случай считается резонансным и решение уравнения при данных параметрах прекращается, если за 100 секунд такого не происходит, то случай считается нерезонансным.

При таком подходе могут быть ошибки с определением того, является ли случай резонансным или нет. Так за 100 секунд амплитуда может возрасти в 39 раз и продолжать расти потом, однако случай ошибочно будет определен как нерезонансный. Эту погрешность определения можно уменьшить, проверяя, возросла ли амплитуда не в 40, а, например, в 10 раз, но в таком случае возникнет другая проблема — амплитуда может возрасти в 10 раз, а потом начать уменьшаться (такой процесс называется биениями), то есть случай будет ошибочно признан резонансным. Биения наблюдаются на границе резонансной зоны и для данной задачи отношение амплитуд равное 40 при биениях не достигается. Таким образом, при автоматическом определении резонанса могут возникать погрешности, не связанные с точностью вычислительной схемы, однако оба явления, описанных выше (биения и слабый резонанс), наблюдаются вблизи границы области резонанса. При исследовании данной задачи, было проверено, что расстояние от точек, в которых могут наблюдаться эти явления, до границы области резонанса заметно меньше, чем шаг, с которым мы изменяем. То есть ошибки, связанные с определением того, является ли случай резонансным, не вносят дополнительной погрешности.

Полученные в итоге результаты согласуются, например, с результатами, приведенными в [9].

3) Термостат Ланжевена.

Наконец рассмотрим уравнение.

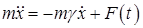
(27).

где — случайная сила, удовлетворяющая следующим условиям:

.

.

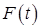
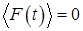
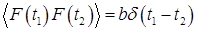
где угловые скобки означают усреднение, а — константа, которая определяется из физических соображений.

Это уравнение описывает термостат Ланжевена, часто использующийся в работах по моделированию физических процессов для приведения системы к нужной температуре. Физически, такое уравнение движения описывает движение частицы, на которую действуют две силы: сила трения и сила упругих соударений с молекулами окружающего нейтрального газа (см. § 1 глава1). Таким образом, константа выбирается в зависимости от типа и плотности нейтрального газа, а константа выбирается так, что бы данное уравнение описывало соударения с молекулами нейтрального газа, находящегося при данной температуре.

Решим данное уравнение относительно скорости.

.

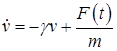
Пусть в начальный момент времени скорость частицы равна. Решение данного уравнения имеет вид.

.

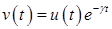
откуда получаем.

.

.

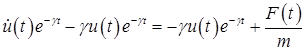
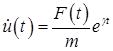
Тогда для скорости получаем следующее выражение.

.

Из него следую два важных соотношения:

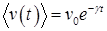
(28).

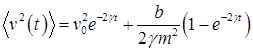
. (29).

Таким образом, среднее значение скорости стремится к нулю с течением времени, а средний квадрат скорости со временем стремится к постоянному значению, равному.

.

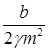
Считая, что кинетическая энергия частицы со временем стремится к тепловой, получаем выражение для константы.

(30).

где — постоянная Больцмана.

Теперь вернемся к численному решению уравнения.

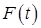
При реализации на компьютере мы будем генерировать случайные значения, подчиняющиеся стандартному нормальному распределению, то есть в уравнении (27) случайную силу надо домножить на коэффициент равный.

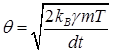
(31).

где — шаг численного интегрирования. Таким образом, мы будем решать уравнение.

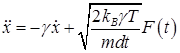
. (32).

График квадрата скорости, полученного при численном решении данного уравнения, и его теоретическое значение.

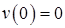
Начальные условия при решении были выбраны как и. После чего было отведено шагов на приведение к равновесию. То есть начало отсчета времени на графике соответствует моменту, когда средний квадрат времени уже приблизился к своему предельному значению.

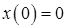
Заметим, что в рассматриваемом случае полная энергия системы равна кинетической энергии движения частицы, случайную силу можно численно воспринимать как случайную погрешность из предыдущего параграфа. Таким образом, предоставленный график не только показывает, что термостат Ланжевена описан верно, но и подтверждает сохранение среднего значения полной энергии. Его сохранение для модели, использующейся в данной работе, будет проверено в следующей главе, после построения самой модели.