Обучение сети.
Создание нейронной сети
Как видно из рисунков, сеть отлично решает поставленную задачу для всех трех выходных параметров. Сохраним обученную сеть net на диске в файл nn1. mat save nn1 net. Следующий шаг — обучение созданной сети. Перед обучением необходимо задать параметры обучения. Задаем функцию оценки функционирования sse. Задаем максимальное количество циклов обучения. После того, как будет выполнено это количество… Читать ещё >
Обучение сети. Создание нейронной сети (реферат, курсовая, диплом, контрольная)
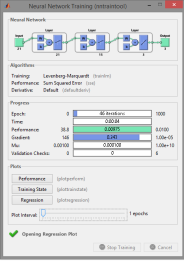
Следующий шаг — обучение созданной сети. Перед обучением необходимо задать параметры обучения. Задаем функцию оценки функционирования sse
net.performFcn='sse';
В этом случае в качестве оценки вычисляется сумма квадратичных отклонений выходов сети от эталонов. Задаем критерий окончания обучения — значение отклонения, при котором обучение будет считаться законченным:
net.trainParam.goal=0.01;
Задаем максимальное количество циклов обучения. После того, как будет выполнено это количество циклов, обучение будет завершено:
net.trainParam.epochs=1000;
Теперь можно начинать обучение:
[net, tr]=train(net, P, T);
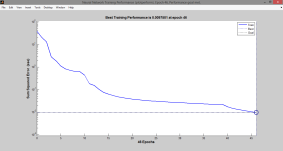
Процесс обучения иллюстрируется графиком зависимости оценки функционирования от номера цикла обучения.
Таким образом, обучение сети окончено. Теперь эту сеть можно сохранить в файле nn1.mat:
save nn1 net;
Тестирование сети
Перед тем, как воспользоваться нейронной сетью, необходимо исследовать степень достоверности результатов вычислений сети на тестовом массиве входных векторов. В качестве тестового массива необходимо использовать массив, компоненты которого отличаются от компонентов массива, использованного для обучения. В нашем случае для получения тестового массива достаточно воспользоваться еще раз программой lab3. сеть массив квадратичный отклонение Для оценки достоверности результатов работы сети можно воспользоваться результатами регрессионного анализа, полученными при сравнении эталонных значений со значениями, полученными на выходе сети когда на вход поданы входные векторы тестового массива. В среде MATLAB для этого можно воспользоваться функцией postreg. Следующий набор команд иллюстрирует описанную процедуру:
y=sim (net, P);
[m, b, r]=postreg (y (1:), T (1:));
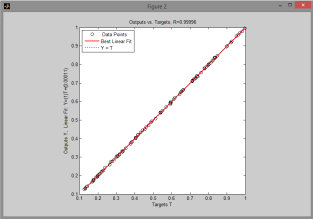
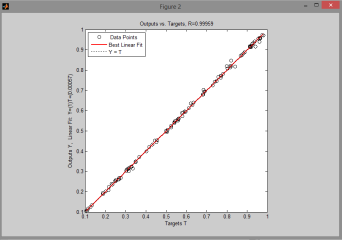
Команда postreg находит параметры линейной зависимости между эталонными значениями, и значениями, вычисленными сетью. Здесь m, b — коэффициенты линейной зависимости y=mT+b; а r — коэффициент линейной регрессии (коэффициент корреляции между y и T).
Видно, что все точки легли на прямую, что говорит о правильной работе сети на тестовом массиве:
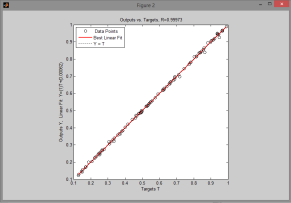
[m, b, r]=postreg (y (2:), T (2:));
[m, b, r]=postreg (y (3:), T (3:));
Как видно из рисунков, сеть отлично решает поставленную задачу для всех трех выходных параметров. Сохраним обученную сеть net на диске в файл nn1.mat save nn1 net