Сущность корреляционного анализа

Часто при исследовании объекта или его модели необходимо наблюдать за характеристиками двух и более случайных величин. Например, за двумя откликами одного эксперимента. При этом может возникнуть вопрос: есть ли связь между этими случайными величинами? Существенна или несущественна эта связь, если она есть?

Корреляционный анализ — это совокупность методов обнаружения зависимости (корреляции) между двумя или более случайными признаками или процессами.

Под корреляцией будем понимать статистическую зависимость между двумя случайными величинами, не имеющую, вообще говоря, строго функционального характера.

Заметим, что корреляционный анализ не позволяет определить вид функциональной связи между случайными величинами, а только наличие или отсутствие предполагаемой связи, например линейной, параболической, экспоненциальной и т. д. В рамках этого учебного пособия мы ограничимся рассмотрением гипотезы о наличии линейной корреляции.

Определение вида функциональной связи между величинами рассматривается в регрессионном анализе, элементы которого и практическое использование будут рассмотрены в параграфе 5.10.

Название «корреляционный анализ» происходит от латинского слова correlado — согласование, связь, соотношение, взаимосвязь. Термин впервые введен Ф. Гальтоном (1822—1911) в 1888 г.

Обычно исследуют парную корреляцию, т. е. зависимость между двумя случайными величинами (процессами), хотя возможны и более сложные ситуации, когда необходимо обнаружить наличие или отсутствие связей между тремя или более случайными величинами.

Мы ограничимся исследованием парной корреляции.

Как известно, связь между двумя случайными величинами можно описать с помощью двумерной функции распределения. Однако такое описание часто очень сложно, а для практических целей можно удовлетвориться определением зависимостей средних значений.

Итак, целью имитационного эксперимента является определение характеристик двух случайных величин а и Ь. Например:

Необходимо проверить: есть ли связь между величинами а и Ь?

Проверка наличия (или отсутствия) связи — корреляции — между случайными величинами выполняется так.

Проводятся два эксперимента, каждый — с соответствующей моделью. В каждом эксперименте — N наблюдений (напоминаем, что компьютерный эксперимент состоит из наблюдений, а наблюдение — из реализаций (прогонов) модели, число которых рассчитывается с учетом требуемой точности и достоверности получаемых результатов моделирования). В результате экспериментов получаются два множества значений измеряемых параметров а и Ь: а_; и Ь_;, i — 1,…, N.

Из этих множеств формируются пары: (а_а, Ь_а), (а₂, Ъ₂), …, (а,-, Ь₍),…, (%, М.

Каждая пара интерпретируется как координаты случайной точки в системе координат а, Ъ.

Первичное исследование можно провести графически. Возможные варианты размещения точек на графиках представлены на рис. 5.5.

Корреляция — важное понятие. Научитесь визуально определять по расположению данных, насколько тесно они коррелированы.

Говорят, что две переменные положительно коррелированы, если при увеличении значений одной переменной увеличиваются значения другой переменной (рис. 5.5, а, б).

Две переменные отрицательно коррелированы, если при увеличении одной переменной другая переменная уменьшается (рис. 5.5, в).

Отсутствие корреляции — совместного поведения переменных — обнаруживается хаотическим нагромождением точек, исключающим проведение какой-либо аппроксимирующей линии (рис. 5.5, г).

Но такого качественного исследования недостаточно. Необходимо иметь количественную оценку степени корреляции между величинами аиЬ.

Если совместное распределение вероятностей случайных величин а и Ъ нормальное, то количественной характеристикой степени линейной связи между ними является коэффициент корреляции г (введен К. Пирсоном в 1896 г.): -1 < г < 1.

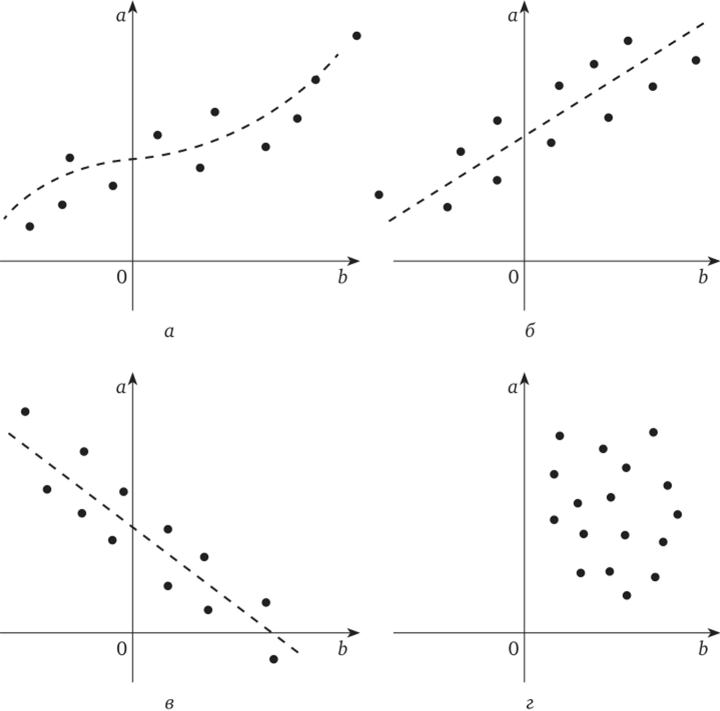
Рис. 5.5. Графическое исследование корреляции:

а — нелинейная зависимость; б — положительная линейная зависимость; в — отрицательная линейная зависимость; г — отсутствие связи Если г = 0, то между а и Ъ линейная независимость.

Равенство г = ± 1 свидетельствует о наличии однозначной функциональной связи между а иЬ, т. е. b = f (a).

При -1 < г < 1 между а и Ъ существует стохастическая связь, причем чем ближе коэффициент корреляции по модулю к единице, тем эта связь сильнее. Стохастическая связь означает, что при изменении а имеется лишь тенденция к изменению Ъ.

Коэффициент корреляции г определяется по данным эксперимента, следовательно, можно определить только его оценку г. В качестве оценки г принят выборочный коэффициент корреляции:

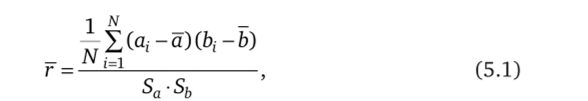
2 N _ ^ N

где а-— У а,-, Ь = — У Ь, — оценки математических ожиданий М (а) N_i=1 AT_i=1

и M (b); S_a = I—Ц-У (а, -а)², S_b = /—-ЦУ (Ь, -Ь)² — оценки средних N —1 ,=1 ] Л/ —1 , _1.

квадратических отклонений a_a и ст_ь.

Выборочный коэффициент корреляции г, так же как и теоретический, принимает значения на отрезке [-1; 1]: -1<�г <1.

Если г > 0, то наблюдается положительная корреляция (см. рис. 5.5, б), если г < 0 — отрицательная корреляция (см. рис. 5.5, в). Если г = 0, то линейная корреляция отсутствует (но не исключена нелинейная). Если г = 1, то между случайными величинами существует жесткая функциональная связь.

Заметим, что рассматриваемый коэффициент корреляции определяет степень линейной связи между случайными величинами, а и Ь. Эта корреляция наиболее популярна, поэтому часто, когда говорят о корреляции, имеют в виду именно корреляцию Пирсона.

Однако этот линейный коэффициент корреляции не является пригодным для оценки нелинейной связи, если таковая присутствует. При нелинейной зависимости степень связи между случайными величинами устанавливается более сложными характеристиками, например корреляционным отношением (К. Пирсон).

Числитель выражения (5.1) иногда называют ковариацией — соv (a, Ь).

Если случайные величины а и b независимы, они и не коррелированы (г =0). Но некоррелированность а и b не всегда свидетельствует об их независимости. Однако если а и b имеют нормальное распределение, то условие г = 0 является необходимым и достаточным условием независимости этих величин.

И еще один момент. Наличие корреляции между случайными величинами а и Ъ не всегда свидетельствует об их взаимосвязи. Дело в том, что при независимости а и Ъ каждая из них в отдельности зависит от некоторого случайного фактора, но эта зависимость нами не замечена.

Поэтому хорошим тоном после вычисления корреляций является построение диаграмм рассеяния, которые позволяют понять, действительно ли между двумя исследуемыми переменными имеется связь.

Оценка коэффициента корреляции должна быть определена с требуемой точностью и достоверностью, которые зависят от числа реализаций модели. Найдем эту связь.

В предположении нормальности распределения г можно написать.

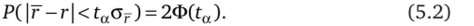
С выражением (5.2) мы уже знакомы. Здесь г — точное значение коэффициента корреляции; о_г — среднее квадратическое отклонение случайной величины r;t_a — аргумент функции Лапласа Ф (с_(Х).

Обычно среднее квадратическое отклонение с₇ неизвестно, поэтому нужно брать его оценку.

При больших выборках N оценка среднего квадратического отклонения S,. такова:

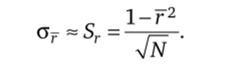
Из формулы (5.2) следуют соотношения.

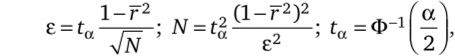
где е — абсолютная величина ошибки.

Предварительное определение г осуществляется по данным пробного эксперимента в количестве N* = 500 + 1000 реализаций модели.

На основании изложенного и в силу случайного характера исследуемых величин а и b мы можем утверждать лишь следующее: истинное значение коэффициента корреляции г лежит в пределах.

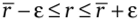
с заданной достоверностью а.

В заключение отметим, что если совместное распределение случайных величин а и b не является нормальным, то оценка г коэффициента корреляции может выступать в качестве ориентировочной оценки степени тесноты связи а и Ь.

Пример 5.7.

Для оценки конструкции нового крупнокалиберного пулемета было произведено 96 выстрелов по щиту, отстоявшему на расстоянии 300 м.

Результаты отклонений попаданий от точки прицеливания (боковые — х₍, по высоте —у,) объединены в десятисантиметровые диапазоны и сведены в таблицу (табл. 5.9).

Таблица 5.9

Отклонения отточки прицеливания

Для оценки конструктивных особенностей пулемета необходимо узнать: есть ли какая-то связь между боковыми отклонениями и отклонениями по высоте?

Решение

Ответ на поставленный вопрос о наличии или отсутствии связи может дать коэффициент корреляции.

Предварительно заметим, что группировка измерений в десятисантиметровые диапазоны вносит некоторую ошибку в дальнейшие расчеты, однако можно показать, что при данной группировке ошибка несущественна.

В табл. 5.9 указаны не реальные отклонения, а центры диапазонов (-25…-15, −15…−5, −5…−5 и т. д.).

Для определения коэффициента корреляции понадобятся следующие.

1 N

характеристики: х, S_x, у, S_y, ковариация —? (х, — х) (у, — у).

Все эти характеристики вычисляются по данным измеренных отклонений — боковых х и по высоте у.

Для примера приведем расчет х:

Результаты расчета остальных характеристик:

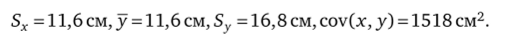
Теперь вычислим оценку коэффициента корреляции:

Среднее квадратическое отклонение этой оценки:

Из-за малого количества выстрелов оценка г определена с ошибкой, которая в предположении о нормальном распределении случайной величины г и достоверности, например, а = 0,8 (С_а = 1,28) равна.

Отсюда следует, что истинное значение коэффициента корреляции г лежит в пределах.

0,082 — 0,128 < г < 0,082 + 0,128, или -0,046 < г < 0,21.

Обнаружена небольшая линейная зависимость отклонений боковых и отклонений по высоте. Баллистики, отвергая непосредственную корреляцию между отклонениями х иу, объясняют значение г > 0 влиянием конструктивных особенностей пулемета. Обнаружена также систематическая ошибка в прицеле: х * 0, у * 0.