Схемотехнические и конструктивные решения системы управления ВТГ

Система возбуждения колебаний резонатора

В работе [5] Журавлева В. Ф. и Линча, основные положения которой приведены в п. 1.5, изложены основные правила управления стоячей волной, позволяющие создать прецизионный ВТГ.

В схеме ВТГ должны функционировать целый ряд систем управления:

• — система возбуждения колебаний резонатора определенной (например, второй моды);
• -система съема информации с емкостных датчиков угла;
• — система стабилизации амплитуды возбужденных колебаний;
• — система фазовой автоподстройки частоты;
• — система подавления квадратурной волны и др.

Дальнейшее изложение материала в настоящей пояснительной записке строится следующим образом: приводится обзор известных технических решений по отдельным системам управления ВТГ (а в разделе 2 — и по конструкциям) и приводится обоснованный выбор технического решения, разрабатываемого по теме. Рассмотрим известные системы возбуждения колебаний резонатора.

Позиционное возбуждение колебаний резонатора ВТГ Рассмотрим принцип и особенности работы системы позиционного возбуждения резонатора ВТГ.

В качестве рабочей формы колебаний в ВТГ используется вторая форма, имеющая четыре узла и четыре пучности. Рассмотрим возникновение рабочей (основной) формы колебаний [16].

Схема позиционного возбуждения показана на рис. 1.6.1. На пару противоположных электродов подается переменное электрическое напряжение с частотой, в 2 раза меньшей, чем собственная частота основной формы:

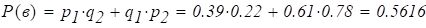
(1.6.1).

Где V0 — амплитуда напряжения; - угловой размер электрода, -собственная частота. График функции V (, 0) показан на рис. 1.6.2.

Поверхности резонатора и электродов покрыты тонким электропроводящим слоем, поэтому они являются обкладками цилиндрического конденсатора. Однако при расчетах можно с хорошей точностью рассматривать такой конденсатор как плоский [16].

Обкладки любого заряженного конденсатора притягиваются, поэтому со стороны электродов на резонатор действуют силы электрического притяжения.

Сила притяжения обкладок плоского конденсатора, отнесенная к площади обкладки, определяется выражением.

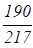
(1.6.2).

где V — разность потенциалов между обкладками; d — расстояние между ними; 0 = 8,85 * 10−12 Ф/м — диэлектрическая постоянная. Знак минус указывает на то, что это всегда сила притяжения.

В соответствии с [16], если вторую гармонику силы притяжения резонатора и электродов возбуждения записать в форме (1.6.3).

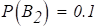
(1.6.3).

где.

 — сила притяжения, нормальная к поверхностям резонатора и электродов,.

 — диэлектрическая постоянная,.

• — квадрат амплитуды приложенного напряжения,
• — угловой размер электрода,
• — собственная частота,

L — высота электрода,.

d — зазор между электродом и резонатором,.

подставить выражение (1.6.3) в правую часть уравнения колебаний (1.4.1) и применить метод Бубнова-Галеркина, то решение уравнения колебаний (1.4.1) можно представить в форме.

(1.6.4).

Выражение для перемещения кромки резонатора можно привести к следующей форме:

(1.6.5).

Производя элементарные преобразования, получаем:

• (1.6.6)
• — угол ориентации стоячей волны в условиях позиционного возбуждения,

m, nамплитуды колебаний кромки резонатора в направлениях под 45 друг к другу.

При = 0 ориентация волнового поля в резонаторе ВТГ постоянна и определяется ориентацией электродов позиционного возбуждения = э, другими словами, стоячая волна «привязана» к корпусу прибора (рис. 1.6.3, а);

при 0 пучность стоячей волны отстает от направления возбуждения на угол , определяемый величиной угловой скорости, собственной частотой и затуханием:

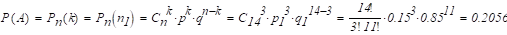
(рис. 1.6.3, б).

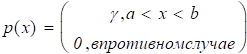
Так как угол отставания стоячей волны пропорционален входной угловой скорости, такой режим работы ВТГ является режимом датчика угловой скорости — ВТГ-ДУС.

Принцип измерения угловой скорости при позиционном возбуждении следующий. На внутренней поверхности резонатора установлены емкостные датчики Д 1 и Д 2 (рис. 1.6.4).

При изменении зазора между поверхностями резонатора и датчика на поверхности датчика появляется избыток заряда, так как разность потенциалов между ней и резонатором неизменна.

Количество заряда пропорционально изменению зазора, т. е. перемещению. Таким образом, сигнал емкостного дачника содержит информацию о перемещении кромки резонатора.

Датчики Д 1 и Д 2 ориентированы под углом 0° и 45°, соответственно. Сигналы, поступающие с них, имеют вид:

датчик Д 1:=m cos t

датчик Д 2: w2 = n sin t

Производя демодуляцию сигналов с опорным сигналом демодулятора sin t, получаем.

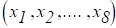
где — ориентация пучности стоячей волны;- сигналы после демодуляции.

Параметрическое возбуждение колебаний резонатора ВТГ Известен принцип работы системы параметрического возбуждения колебаний резонатора ВТГ. В [16] показано, что в этом случае ВТГ выполняет функцию интегратора угловой скорости или датчика угла поворота основания, на котором установлен гироскоп, т. е. ВТГ работает в режиме интегрирующего гироскопа (ВТГ-ИГ) или в режиме «свободного гироскопа» .

Параметрическое возбуждение осуществляется с помощью кольцевого электрода, окружающего кромку резонатора. Поверхности резонатора и кольцевого электрода можно рассматривать как обкладки цилиндрического конденсатора, к которым приложено напряжение, не зависящее от угла , с частотой, близкой к собственной частоте резонатора V=V0 cos 2t.

Назначение системы параметрического возбуждения — компенсация энергетических потерь резонатора, определяемых, главным образом, внутренней диссипацией материала резонатора и влиянием остаточного газа в приборе. Система позиционного возбуждения для этой цели не подходит, так как стоячая волна будет «затягиваться» к электродам возбуждения На рис. 1.6.5 показан процесс параметрического возбуждения. Когда резонатор не деформирован, электрические силы уравновешены внутренними напряжениями. Когда резонатор деформируется, то притягивающая сила в области меньшего зазора увеличивается, а сила в области большего зазора уменьшается, так как эта сила обратно пропорциональна квадрату величины зазора между кольцевым электродом и резонатором. Результирующая сила приводит к еще большей деформации резонатора и действует в направлении пучностей стоячей волны.

Четыре фрагмента рис. 1.6.5 иллюстрируют этот процесс. На фрагменте 1 резонатор движется в сторону максимальной деформации, напряжение питания включено. На фрагменте 2 резонатор по инерции возвращается в положение равновесия, при этом напряжение отключено. На фрагментах 3 и 4 этот порядок повторяется, но в противоположную сторону.

При изменении напряжения с частотой, равной собственной частоте резонатора по основной форме, происходит параметрическое возбуждение резонатора.

Для расчета примем, что касательная составляющая электрической силы, приложенной к резонатору, равна нулю, а нормальную разложим в ряд по степеням перемещения w с точностью до первого порядка:

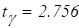
где многоточие обозначает величины более высокого порядка малости, а также постоянную составляющую.

С учетом сказанного запишем уравнение динамики кольцевой модели резонатора в условиях параметрического возбуждения, соответствующее уравнению (1.4.1).

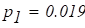
(1.6.7).

Решение уравнения (1.6.7) представим в форме.

(1.6.8).

Подставляя (1.6.8) в (1.6.7) и применяя метод Бубнова — Галеркина, приходим к системе:

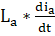
(1.6.9).

Пусть = (t) — медленная функция времени, т. е. функция, скоростью изменения которой можно пренебречь. Введем медленные переменные а(t), m (t), bit), n (t), согласно следующим условиям:

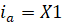
(1.6.10).

Подставляя (1.6.10) в (1.6.9) и производя осреднение полученной системы по быстрой переменной t [ 3], приходим к системе, описывающей эволюцию медленных переменных:

(1.6.11).

где.

;

2 — близко к собственной частоте 0.

Построим границу области устойчивости системы (1.6.11) при = 0.

Для существования ограниченных колебаний в системе (1.6.11) при = 0 необходимо и достаточно, чтобы выполнялось равенство.

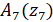
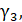
(1.6.12).

Условие (1.6.12) дает уравнение границы области устойчивости в плоскости параметров и s;

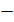
(1.6.13).

Уравнение (1.6.13) определяет гиперболу (рис. 1.6.6), причем точка минимума имеет координаты:

(1.6.14).

Область внутри гиперболы соответствует неустойчивым колебаниям, область вне гиперболы устойчивым колебаниям.

Рассмотрим случай режима возбуждения с частотой и амплитудой напряжения кольцевого электрода, соответствующими точке минимума (1.6.14):

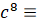
(1.6.15).

По отношению к амплитуде подаваемого напряжения этот режим является оптимальным.

Колебательный процесс, возбужденный в резонаторе, запишем в следующем виде:

(1.6.16).

В работе [3] показано, что (1.6.16) будет представлять собой стоячую волну при выполнении условия:

I (1.6.17).

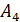
Запишем систему (1.6.11), теперь при 0. при условии (1.6.14).

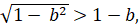
(1.6.18).

Далее в силу (1.6.17) решение (1.6.16) преобразуется к виду.

(1.6.19).

где tg = т/а; tg 2 =.

Угол определяет ориентацию стоячей волны (1.6.19) относительно резонатора. Для нахождения эволюции этого угла имеем соотношение.

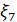
Вычисляя производную и пользуясь уравнениями системы (1.6.18), получаем.

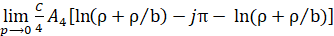
Выражение в квадратных скобках равно нулю, поэтому.

.

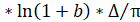
где К=0,4 — масштабный коэффициент.

Из последней формулы следует, что угол поворота стоячей волны пропорционален углу поворота корпуса ВТГ, т. е. в режиме параметрического возбуждения BТГ является интегрирующим (ВТГ-ИГ).

Угол находится с помощью демодуляции с опорным сигналом из формулы (1.6.19). Сигналы с датчиков Д 1 и Д 2 имеют вид:

датчик Д 1: ;

датчик Д 2:, (1.6.20).

где.

После проведения демодуляции сигналы преобразуются следующим образом:

;

. (1.6.21).

Отсюда находим, что.

.

Угол поворота основания равен:

. (1.6.22).