Оптимизация специальной силовой физической подготовки спортсменов с помощью переменного отягощения

Практика спорта и экспериментальные исследования [4] показывают, что одним из самых эффективных средств специальной физической подготовки спортсменов является соревновательное упражнение. В работах Бернштейна Н. А., Донского Д. Д., Зациорского В. М., Фельдмана А. Г. обращается внимание на то, что движения, подчиняясь законам механики, обладают сложной внутренней структурой управления, настраивающей мышечную систему человека на эффективное и экономичное взаимодействие с внешними и внутренними силами.

Важным направлением является изучение биомеханических показателей спортивных движений для повышения эффективности тренировочного процесса [1]. Выполнение соревновательного упражнения с максимальной нагрузкой связано с большими затратами физической и нервной энергии, особенно, когда преодолевается пик нагрузки [4].

При выполнении приседаний, рывковых и тяговых упражнений со штангой в начале упражнения проявляется максимальная нагрузка, когда плечи сил, проявляемых мышцами нижних конечностей невелики. В результате такой нагрузки на мышцы, посредством которых выполняются упражнения со штангой в тяге при приседании или в рывке, воздействие на мышцы оказывается неравномерным. Максимального эффекта от силового воздействия можно достичь, если изменять величину внешней нагрузки таким образом, чтобы мышцы, на которые направлено тренировочное воздействие, проявляли максимальную силу не только в начале движения, но и на всем пути при выполнении упражнений.

Проведя биомеханический анализ движения в суставах в процессе выполнения упражнения, было установлено, что наибольшее изменение плеча силы наблюдалось при сокращении больших ягодичных мышц.

Цель исследования состояла в определении внешних условий при создании постоянной нагрузки, с учетом изменения плеча силы больших ягодичных мышц при разгибании тазобедренного сустава человека во время выполнения тяги штанги.

Длина и сила мышц — это основные внешние механические характеристики мышцы. Анатомо-геометрические параметры тела человека влияют на величину проявляемой силы, так как угол в суставе меняет длину мышцы и ее плечо. М. gluteus maximus (рис. 1) является «донором» механической энергии для коленного и голеностопного суставов, поэтому для повышения мощности отталкивания необходимо уделять внимание не только развитию силы мышц — разгибателей коленного и голеностопного суставов, но и мышц — разгибателей тазобедренных суставов. Так как мышцы разгибатели коленного сустава имеют постоянное плечо силы, то мышцы голеностопного сустава вносят незначительный вклад в разгибание звеньев тела при воздействии на него внешней нагрузки.

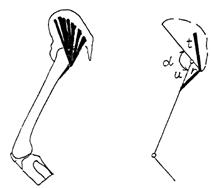
Рисунок 1. Анатомическое расположение и модель m. gluteus maximus.

Рассмотрим, как меняется плечо силы больших ягодичных мышц (рис. 2) при их сокращении и выполнении разгибания в тазобедренном суставе, когда угол между туловищем и бедром меняется от 60 до 120 град., что соответствует первой половине движения, когда из-за меняющегося плеча силы рассматриваемой мышцы, нагрузка на нее наиболее неравномерна.

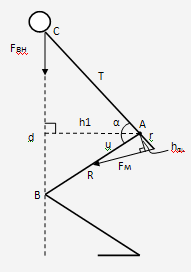
Рисунок 2. Определение плеча силы hGL и плеча силы h1:

R — длина бедра;

Т — длина туловища (от тазобедренного сустава до места приложения силы F_вн);

F_вн — внешняя сила (масса штанги);

F_м — сила тяги больших ягодичных мышц;

h_GL -плечо силы F_м;

h₁ — плечо силы F_вн;

r — расстояние от центра вращения в тазобедренном суставе до края седалищного бугра, см;

u — расстояние от центра вращения в тазобедренном суставе до места прикрепления m. gluteus maximus на бедренной кости, см;

б — угол между туловищем и бедром, град Плечо силы m. gluteus maximus h_GL можно найти по формуле [2]:

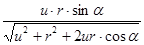
h_GL=, где.

h_GL — плечо силы m. gluteus maximus, см;

Величины u и r выбраны в соответствии с исследованиями [2] и равны.

u = 11,9 см., r = 2,9 см.

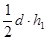
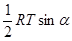
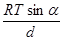
Силе исследуемой мышцы, которая разгибает туловище при выполнении тяги, противодействует вес штанги с плечом силы h₁ (рис.2). Найдем h₁ из? АВС, зная длину туловища Т, длину бедра R и угол между ними б. С одной стороны площадь? АВС равна, с другой. Приравняв эти два выражения, выразим h₁: h₁ =, где.

d — перемещение той части туловища, на которую действует внешняя нагрузка при выполнении упражнения.

Используя зависимость.

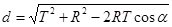
можно перейти от двойной зависимости h₁(б, d) к h₁(d) и от h_GL (б) к h_GL (d).

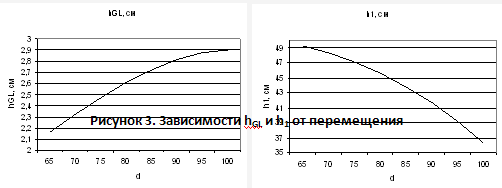
Рисунок 3. Зависимости hGL и h1 от перемещения.

Из полученных зависимостей (рис. 3) видно, что при выполнении движения с увеличением d плечо h_GL силы Fм увеличивается, а плечо h₁ силы F_вн уменьшается.

Если считать, что ускорение движения штанги при выполнении тяги близко к нулю, то момент силы со стороны ягодичных мышц h_GL F_м можно считать равным моменту сил со стороны внешней нагрузки h₁?F_вн, роль которой выполняет штанга при выполнении тяги, т. е.

h₁?F_вн = h_GL F_м

Из этого равенства можно выразить силу, которую проявляют ягодичные мышцы при выполнении упражнения с постоянной нагрузкой.

F_м= F_вн

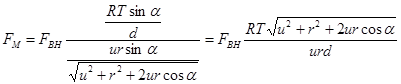
Полученное распределение силы F_м имеет нелинейную зависимость, то есть при выполнении упражнения в начале пути нагрузка на ягодичные мышцы максимальна, и в процессе выполнения упражнения она уменьшается (рис. 4).

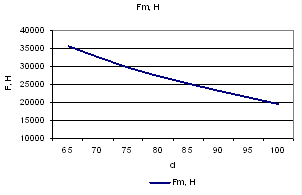
Рисунок 4. График силы, проявляемой ягодичными мышцами в зависимости от перемещения.

В процессе тренировки при силовом взаимодействии спортсмена со штангой при выполнении упражнения тяги была поставлена задача поддерживать величину нагрузки постоянной. Отобразив зеркально зависимость F_м(d), мы получили график, компенсирующий нелинейность F_м(d) так, чтобы мышцы, разгибающие туловище, имели постоянную величину нагрузки.

Для решения этой задачи с целью создания внешней нагрузки был использован тренажер [4], в котором выбор режима нагрузки можно обеспечить выбором углового положения рычага, массы груза на рычаге, массы штанги и длины рычага.

Чтобы найти эти параметры, используем математическую модель тренажера [3].

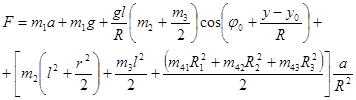
где — масса штанги, — масса груза, — масса рычага;

— радиусы трех звездочек;

— их массы;

— ускорение штанги;

? — длина рычага.

Зависимость угла, отсчитываемого от горизонтали против часовой стрелки от положения штанги:

.

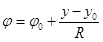
где — один из радиусов, на который накинута цепь.

Так как ускорение близко к нулю, то первым и последним слагаемыми в уравнении математической модели тренажера можно пренебречь.

Чтобы определить угловое положение рычага, массу груза на рычаге, массу штанги и длину рычага, необходимо решить уравнение:

F_м+ F_вн =const, где константой является та постоянная нагрузка, которая должна воздействовать на тренируемые мышцы. Решив это уравнение численно для примера (Т=75 см, R=50 см, r=2,9 см, u=11,9 см, const=100 кг), рассчитанная нагрузка (рис. 5) реализуется при ц=53°; m₁=160кг m₂=30кг;=48см.

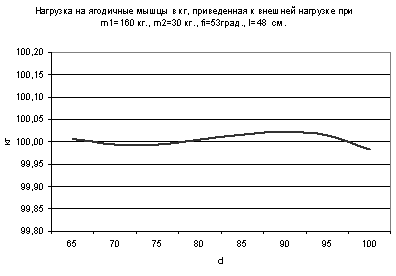
Рисунок 5. График силы, проявляемой ягодичными мышцами, с использованием тренажера.

Сила, воздействующая на ягодичные мышцы и приведенная численно к внешней нагрузке при таких условиях, находится практически на уровне 100 кг на всем пути выполнения упражнения (рис. 6).

На рисунке 6 приведен график силы, скорректированной с помощью тренажера, которую будут проявлять большие ягодичные мышцы выполнении тяги со штангой. Относительное постоянство нагрузки при перемещении штанги (рис. 5) позволяет более полноценно обеспечивать рабочую мышцу нагрузкой, что повышает эффективность силовой подготовки.

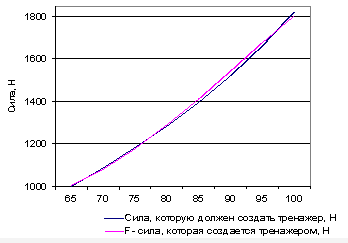
Рисунок 6.

• 1. Доронин А. М. Скоростно-силовая подготовка спортсменов с использованием машины управляющего воздействия: Автореф. дисс… канд. пед. Наук / А. М. Доронин. — М.: Физкультура и спорт, 1992. — 19 с.
• 2. Самсонова А. В. Моторные и сенсорные компоненты биомеханической структуры физических упражнений [электронный курс]: Дис. д-ра. пед. наук: 13.00.04 / А. В. Самсонова. — М.: РГБ, 2003. (Из фондов Российской государственной библиотеки)
• 3. Мамий А. Р., Поляков С. В. Математическая модель машины управляющего воздействия. Труды ФОРА, № 5, 2000, с. 56−60.
• 4. Черкесов Ю. Т. Управление становлением двигательных умений тяжелоатлетов при использовании методических приемов, основанных на применении технических средств: Атореф. дисс… канд. пед. наук / Ю. Т Черкесов. — М.: Физкультура и спорт, 1979. — 21 с.