Представление синусоидальных величин с помощью векторов и комплексных чисел

Представление синусоидальных величин с помощью векторов и комплексных чисел Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися — переменными — токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т. д.) называется ток (напряжение, ЭДС и т. д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока имеем.

(1).

Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):

(2).

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01ё 10 Гц — в системах автоматического регулирования, в аналоговой вычислительной технике) — до сверхвысоких (3000ё 300 000 МГц — миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i — мгновенное значение тока ;

u — мгновенное значение напряжения ;

е — мгновенное значение ЭДС ;

р — мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).

— амплитуда тока;

— амплитуда напряжения;

— амплитуда ЭДС.

Действующее значение переменного тока Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

(3).

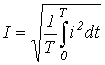
Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных ЭДС, напряжений и токов на плоскости декартовых координат Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е₁ и е₂ соответствуют уравнения:

.

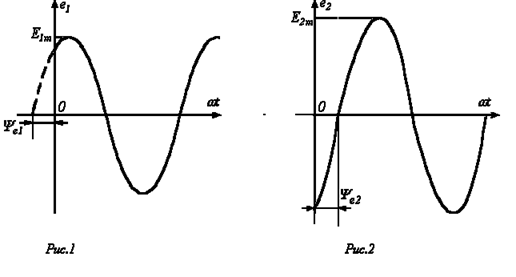
Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени (t=0): и — начальной фазой ().

Величину, характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть.

.

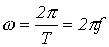
где f — частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.

Для синусоидальных ЭДС е₁ и е₂ угол сдвига фаз:

.

Векторное изображение синусоидально изменяющихся величин На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂ (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

.

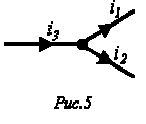
Каждый из этих токов синусоидален и может быть представлен уравнением и.

Результирующий ток также будет синусоидален:

.

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.

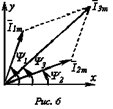
На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

.

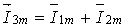
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты:

.

Представление синусоидальных ЭДС, напряжений и токов комплексными числами Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в:

показательной.

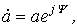
тригонометрической или алгебраической — формах.

Например, ЭДС, изображенной на рис. 7 вращающимся вектором, соответствует комплексное число.

.

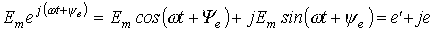
Фазовый угол определяется по проекциям вектора на оси «+1» и «+j» системы координат, как.

.

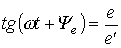
В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:

(4).

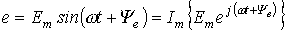
Комплексное число удобно представить в виде произведения двух комплексных чисел:

(5).

Параметр, соответствующий положению вектора для t=0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой:, а параметр — комплексом мгновенного значения.

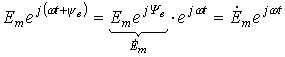
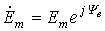
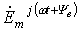
Параметр является оператором поворота вектора на угол wt относительно начального положения вектора.

Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ±a.

Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака «j» произведения комплекса амплитуды и оператора поворота :

.

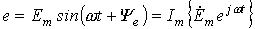
Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:

(6).

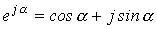
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:

.

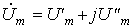
— то для записи ее в показательной форме, необходимо найти начальную фазу, т. е. угол, который образует вектор с положительной полуосью +1:

.

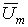
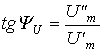
Тогда мгновенное значение напряжения:

.

.

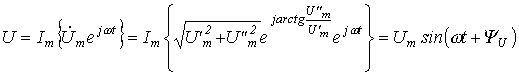
При записи выражения для определенности было принято, что, т. е. что изображающий вектор находится в первом или четвертом квадрантах. Если, то при (второй квадрант).

(7).

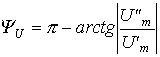
а при (третий квадрант).

(8).

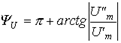
или.

(9).

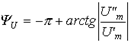
Если задано мгновенное значение тока в виде, то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:

.

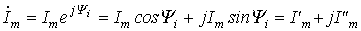
Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.

Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:

;

.

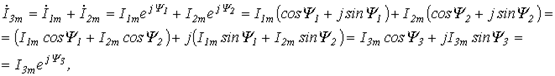
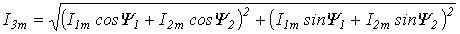
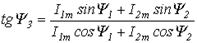
Действующее значение синусоидальных ЭДС, напряжений и токов В соответствии с выражением (3) для действующего значения синусоидального тока запишем:

.

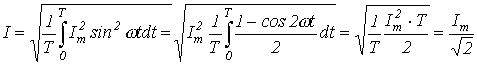
Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз:

. (10).

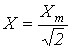
Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения.

.

Литература

напряжение ток амплитуда.

• 1. Основы теории цепей: Учеб. для вузов /Г.В. Зевеке, П. А. Ионкин, А. В. Нетушил, С. В. Страхов. -5-е изд., перераб. — М.: Энергоатомиздат, 1989. -528 с.
• 2. Бессонов Л. А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. -7-е изд., перераб. и доп. — М.: Высш. шк., 1978. — 528 с.