Ранговая корреляция. 
Теория вероятностей и математическая статистика для экономистов

Для анализа связей между признаками, измеренными в порядковых шкалах, применяют так называемые ранговые коэффициенты корреляции Спирмена и Кенделла. Расчет рангового коэффициента корреляции Спирмена производится по формуле.

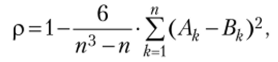
где A_k — ранг k-vo наблюдения признака X, B_k — ранг k-vo наблюдения признака У, а п — число пар наблюдений. Данный коэффициент изменяется в пределах от -1 до +1.

Проверка статистической значимости данного показателя осуществляется с помощью статистики t

Так же как и для линейного коэффициента корреляции, при условии отсутствия связи данная статистика распределена по закону Стьюдента с (п — 2) степенями свободы. Вычисленную по формуле (11.4) статистику сравнивают с соответствующим критическим значением распределения Стьюдента. Если она не превосходит критического значения, то считают, что рассчитанный ранговый коэффициент корреляции статистически незначим.

Пример 11.3. По 10 предприятиям имеются следующие статистические данные:

Рассчитаем ранговый коэффициент корреляции Спирмена и сделаем выводы. Решение. Для удобства расчеты представим в таблице:

Подставляя полученные значения в формулу коэффициента корреляции рангов Спирмена, получим.

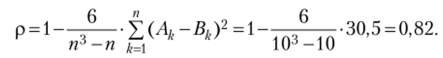
Согласно шкале Чсддока связь между данными признаками высокая.

Проверим значимость рангового коэффициента корреляции с помощью статистики ?. В нашем случае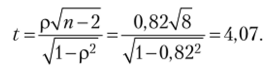

Используя функцию СТЬЮДРАСПОБР в MS Excel, находим критическое значение, отвечающее числу степеней свободы п — 2 = 10 — 2 = 8 и уровню значимости, а = 0,05. Оно равно ?_та6л= 2,31. Поскольку вычисленное значение больше критического, то считается, что найденный ранговый коэффициент корреляции статистически значим.

Еще одной мерой связи между признаками х и у является коэффициент корреляции рангов Кенделла.

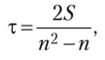
где 5 — сумма баллов, если баллом +1 оценивается пара рангов, имеющих по обоим показателям одинаковый порядок, а баллом -1 — пара рангов с разным порядком. Данный коэффициент изменяется в пределах от -1 до +1.

Расчет коэффициента корреляции рангов Кенделла можно упростить следующим образом.

• 1. Записываем ранги по признаку X в возрастающем порядке с указанием соответствующих им рангов, но признаку У.
• 2. Подсчитываем баллы для всех рангов, но признаку У. Для этого находим, сколько рангов, предшествующих каждому рангу и последующих за ним, превышают его величину. Число предшествующих превышений записываем со знаком «минус», а число последующих превышений — со знаком «плюс».
• 3. Находим сумму положительных и отрицательных баллов по каждому рангу и итоговое число баллов 5.
• 4. Далее действуем по указанной формуле.

Пример 11.4. Рассчитаем коэффициент корреляции рангов Кснделла на основе данных предыдущего примера 11.3, используя полученные ранги статистических данных.

Решение. Для удобства расчеты представим в таблице, записав ранги по признаку X в возрастающем порядке с указанием соответствующих им рангов по признаку У:

Таким образом, сумма баллов 5 = 30. Подставляем значения в формулу и получаем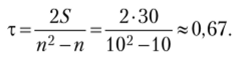

Величина рангового коэффициента корреляции Кенделла также свидетельствует о прямой, довольно тесной связи между рассматриваемыми признаками.

Значительная часть признаков, измеренная с помощью номинальных шкал, составляет дихотомические признаки, принимающие два и более альтернативных значений. При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативного признака, составляется таблица четырех полей (табл. 11.2).

Таблица 11.2

Таблица четырех полей

На основе таких таблиц рассчитываются два показателя: коэффициент ассоциации и коэффициент контингенции.

Коэффициент ассоциации рассчитывается по формуле.

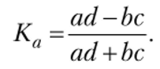
Предельным значением для коэффициента ассоциации является 0,5, т. е. если К_а > 0,5, то между признаками имеется существенная взаимосвязь.

Коэффициент контингенции рассчитывается по формуле.

Если K_k > 0,3, то считается, что между признаками существует корреляционная связь.

Коэффициенты ассоциации и контингенции изменяются от -1 до +1, и чем ближе они к -1 или к +1, тем сильнее связаны между собой изучаемые признаки. Коэффициент контингенции всегда меньше коэффициента ассоциации.

Пример 11.5. Для оценки связи между ростом и весом студентов определим коэффициенты ассоциации и контингенции и сделаем вывод на основе сведений, представленных в таблице.

Решение. Имеем: а = 305; fe = 17;c = 112;rf = 67.

Тогда коэффициент ассоциации равен.

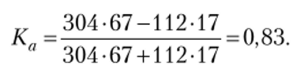
Так как полученное значение по абсолютной величине явно превышает пороговое значение 0,5, то можно сделать вывод о существовании статистической взаимосвязи между изучаемыми признаками.

Рассчитаем коэффициент контингенции:

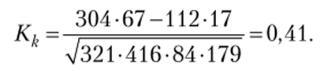
Так как полученное значение, но абсолютной величине превышает пороговое значение 0,3, то можно сделать вывод о существовании статистической взаимосвязи между изучаемыми признаками.

В соответствии со шкалой Чеддока между ростом и весом студентов существует взаимосвязь от умеренной до высокой.