Методы вероятностной выборки

Для начала несколько определений: выборка — часть генеральной совокупности, извлекаемая для анализа; генеральная совокупность — множество всех рассматриваемых объектов. Вместо того, чтобы изучать всю совокупность объектов, изучают выборку, а затем результаты, полученные на выборке, распространяют на всю совокупность. Выборочные исследования занимают меньше времени, они дешевле, проще и практичнее, чем полное исследование. Например, вместо осуществления полной переписи населения, статистические процедуры выборочного исследования концентрируют внимание на сборе информации о малой репрезентативной группе, взятой из большой генеральной совокупности. Выборка, полученная в результате этих процедур, содержит информацию, которую можно использовать для оценки свойств всей генеральной совокупности.

Процедура выбора начинается с определения основы, представляющей собой полное или частичное перечисление объектов, содержащихся в генеральной совокупности. Основой могут служить источники данных, например, списки населения, каталоги или карты. Затем из основы извлекаются выборки. Если основа является неадекватной, например, вследствие того, что лица или объекты, принадлежащие генеральной совокупности, выбраны неправильно, то выборки будут неточными и тенденциозными. Существует два вида выборок: детерминированные и вероятностные (рис. 1).

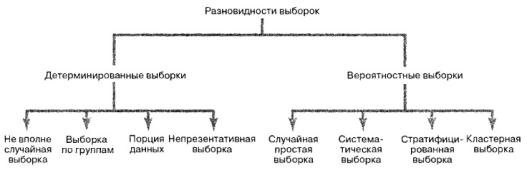
Рис. 1. Разновидности выборок

Детерминированная выборка состоит из элементов, включенных в нее без учета вероятности их появления. Поскольку детерминированные выборки содержат элементы без учета вероятности их появления, причем в некоторых случаях респонденты участвуют в опросах по собственной инициативе, к ним нельзя применить теорию, разработанную для вероятностных выборок. Типичным примером детерминированных выборок являются нерепрезентативные выборки. Объекты включаются в такие выборки на основе соображений простоты, дешевизны или удобства отбора. Например, многие компании проводят опросы, предоставляя посетителям их Web-страниц возможность заполнить анкету. Такие анкеты позволяют собрать большое количество информации за короткий промежуток времени, однако выборки состоят из ответов пользователей Интернета, которые принимают участие в опросе по собственной инициативе. [c. 150].

Нерепрезентативные выборки обладают некоторыми преимуществами, в частности, их можно легко и быстро создавать, не расходуя больших средств. С другой стороны, у них есть два важных недостатка — низкая точность, являющаяся следствием тенденциозности, и ограниченность результатов. Преимущества детерминированных выборок не компенсируют их недостатки. Следовательно, детерминированные выборки следует применять лишь для грубых и недорогих оценок, предназначенных для удовлетворения любопытства, либо в качестве учебного или пилотного проекта, который подлежит дальнейшему уточнению.

Вероятностная выборка состоит из элементов, вероятность появления которых известна заранее. Вероятностные выборки следует применять всегда, когда это возможно, поскольку лишь они позволяют сделать корректные статистические выводы о генеральной совокупности. На практике получить истинно вероятностную выборку очень трудно или просто невозможно. Однако для создания вероятностной выборки необходимо следовать правилам и учитывать любую возможную тенденциозность. Существует четыре вида вероятностных выборок: простая случайная, систематическая, стратифицированная и кластер. Каждой из этих выборок соответствует свой метод выбора, который характеризуется собственной стоимостью, точностью и сложностью.

Простая случайная выборка. Вероятность выбора элементов простой случайной выборки из основы совпадает с вероятностью выбора любого другого элемента. Кроме того, вероятность извлечения из основной совокупности любых выборок фиксированного объема является постоянной для данного объема. Простой случайный выбор представляет собой элементарную процедуру, на основе которой создаются более сложные методы выбора.

В рамках простого случайного выбора символом n обычно обозначают объем выборки, а символом N — объем основы. Каждый элемент основы нумеруется числами от 1 до N. Вероятность выбрать любой конкретный элемент основы при первом извлечении равна1/N. Существует два основных способа извлечения выборок: с возвращением и без него.

Выбор с возвращением означает, что выбранный элемент возвращается в основу, причем вероятность его повторного извлечения остается постоянной. Представьте себе урну, в которой находятся 100 визитных карточек. Допустим, что при выборе первого элемента мы извлекли визитную карточку Джуди Крэйвен. Отметим этот факт в своих записях и вернем карточку в урну. Перемешаем карточки, а затем извлечем из урны вторую визитку. При втором испытании вероятность извлечь визитную карточку Джуди Крэйвен остается равной 1/N. Процесс продолжается до тех пор, пока не будет достигнут желаемый объем выборки n. Однако часто более предпочтительным является способ, при котором выборки не содержат повторяющихся элементов.

Выбор без возвращения означает, что после извлечения элемент не возвращается в основу и, следовательно, не может быть выбран вновь. При первом извлечении элемента вероятность его выбора из основы равна 1/N. Однако, в отличие от выбора с возвращением, вероятность выбора элемента, не извлеченного при первом испытании, равна 1/(N-1). Процесс продолжается до тех пор, пока не будет достигнут желаемый объем выборки n. Независимо от схемы выбора (с возвращением или без), такой подход имеет один существенный недостаток — он зависит от тщательности перемешивания элементов и случайности их выбора. Поэтому метод урн считается не вполне приемлемым. Желательно применять более простой и научно обоснованный метод выбора элементов. Один из таких методов основан на таблице случайных чисел, состоящей из последовательности цифр, сгенерированных случайным образом.

Excel предоставляет, наверное, наиболее простой метод генерации случайных чисел. Для этих целей у него есть две функции: =СЛУЧМЕЖДУ (нижн_граница; верхн_граница) — возвращает случайное число между двумя заданными числами (рис. 2); =СЛЧИС () — возвращает равномерно распределенное случайное число большее или равное 0 и меньшее 1 (рис. 3). Надо заметить, что при каждом изменении на листе Excel случайные числа пересчитываются.

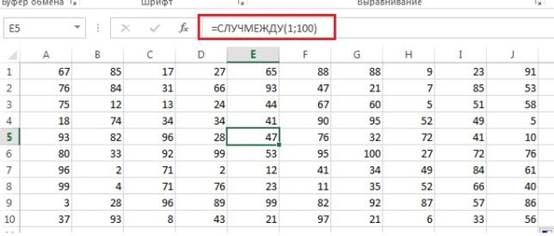
Рис. 2. Случайные числа в диапазоне от 1 до 100, сгенерированные в Excel с помощью функции СЛУЧМЕЖДУ.

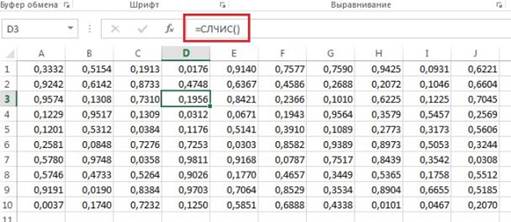
Рис. 3. Случайные числа в диапазоне от 0 до 1, сгенерированные в Excel с помощью функции СЛЧИС; показаны только четыре знака после запятой.

Для того чтобы воспользоваться генератором случайных чисел, необходимо сначала присвоить элементам основы соответствующий числовой код. Например, некая компания оплачивает своим сотрудникам стоматологическую помощь и желает оценить свои затраты. Для этого необходимо извлечь из генеральной совокупности, состоящей из 800 постоянных сотрудников, случайную выборку, объем которой равен 32. Компания предполагает, что не каждый сотрудник захочет добровольно принять участие в опросе, поэтому завышает объем выборки, чтобы в случае отказа в ней осталось хотя бы 32 человека. Предполагая, что в опросе примут участие 8 сотрудников из каждых 10 (т.е. 80% персонала), можно утверждать, что для создания выборки, состоящей из 32 сотрудников, необходимо опросить как минимум 40. Следовательно, анкету следует распространить среди 40 сотрудников, произвольным образом выбирая их личные дела. Как организовать простой случайный выбор?

Расположите фамилии сотрудников по алфавиту, присвойте каждому номер от 1 до 800, выделите в Excel область, включающую 40 ячеек, в каждой из которых поместите формулу =СЛУЧМЕЖДУ (1;800). Раздайте анкету сотрудникам, под соответствующими номерами (рис. 4).

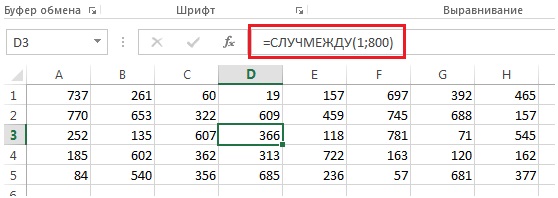
Рис. 4. Номера для выбора 40 сотрудников

Систематическая выборка. При формировании систематической выборки N элементов, образующих основу, разбиваются на k групп, имеющих объем n. Иначе говоря, k = N/n. Число k округляется до ближайшего целого числа. Чтобы получить систематическую выборку, ее первый элемент нужно случайным образом выбрать из первых k элементов первой группы, взятой из основы. Остальные элементы образуются путем выбора каждого k-гo элемента всей основы.

Если основа состоит из списка пронумерованных чеков, квитанций или счетов либо списка членов клуба, студентов и т. п., систематическую выборку легче и проще получить с помощью простого случайного выбора. В этих ситуациях систематическая выборка является удобным механизмом для получения желаемых данных. c. 326].

Если систематическая выборка, состоящая из 40 элементов, должна быть образована из генеральной совокупности, в которую входят 800 сотрудников, основу необходимо разделить на 20 групп (800/40=20). Среди первых 20 кодов следует выбрать случайное число, а затем включить в выборку каждый 20-й элемент основы. Например, если в качестве первого случайного числа выбран код 008, следующими элементами должны стать сотрудники с номерами 028, 048, 068, 088, 108, …, 768и 788.

Несмотря на свою простоту, методы простого случайного и систематического выбора обычно менее эффективны, чем другие, более сложные методы получения вероятностных выборок. Это значит, что данные, полученные с помощью простого или систематического выбора, не всегда хорошо отражают свойства всей генеральной совокупности. Хотя метод простого выбора теоретически позволяет правильно оценить свойства генеральной совокупности, в каждом конкретном случае невозможно определить, является ли та или иная выборка репрезентативной.

Систематические выборки чаще бывают более неадекватными и нерепрезентативными, чем выборки, сформированные путем простого случайного выбора. Если в основе существует определенная структура, может возникнуть систематическая ошибка. Для решения потенциальной проблемы неадекватности специфических групп, входящих в выборку, применяется либо метод стратифицированного выбора либо метод кластерного выбора.

Стратифицированная выборка. При формировании стратифицированной выборки N элементов генеральной совокупности или основы разделяются на отдельные подмножества, или страты, обладающие общими свойствами. Затем к каждому подмножеству применяется простой случайный выбор, и его результаты объединяются в одно целое. Этот метод выбора более эффективен, чем методы простого или систематического выбора, поскольку он обеспечивает большую репрезентативность выборки. Точность оценки параметров генеральной совокупности гарантируется однородностью элементов, принадлежащих одному подмножеству.

Например, некая компания оплачивает своим сотрудникам стоматологическую помощь и желает оценить свои затраты. Для этого необходимо извлечь из генеральной совокупности, состоящей из 800 постоянных сотрудников, случайную выборку, включающую в себя 32 человека. Компания предполагает, что ответы дадут лишь 80% тех, кому выдадут анкеты, поэтому необходимо опросить как минимум 40 человек. Как извлечь стратифицированную выборку?

Основа представляет собой список имен и учетных номеров всех 800 сотрудников. Поскольку 25% постоянных сотрудников относится к управляющему персоналу, сначала необходимо разделить основу на две страты: подмножество, состоящее из 200 менеджеров, и подмножество, включающее в себя 600 остальных сотрудников. Поскольку первая страта состоит из 200 менеджеров, код каждого менеджера задается трехзначным числом от 001 до 200. Аналогично, поскольку вторая страта состоит из 600 сотрудников, каждому из них присваивается трехзначный код от 001 до 600.

Для того чтобы создать стратифицированную выборку, необходимо выбрать из первой страты 25% выборки, а остальные 75% извлечь из второй страты. Следовательно, достаточно дважды применить простой случайный выбор элементов из каждой страты, как описано выше. Возникнут две простые случайные выборки. Первая из них состоит из 10 сотрудников, извлеченных из первой страты, а вторая — из 30 сотрудников, принадлежащих второй страте. Выборка, полученная в результате этой процедуры, будет правильно отображать структуру компании.

Кластерная выборка. Для образования кластерной выборки основа, состоящая из N элементов, разбивается на несколько кластеров так, чтобы каждый кластер отражал свойства всей генеральной совокупности. Затем осуществляется простой случайный выбор кластеров, в которых изучаются все элементы. Кластеры естественным образом получаются при статистическом анализе округов, избирательных участков, городов, районов или семей.

Метод кластерного выбора может оказаться менее дорогостоящим, чем метод простого случайного выбора, особенно если генеральная совокупность распределена по широкому географическому региону. Однако метод кластерного анализа в целом менее эффективен, чем методы простого случайного и систематического выбора, и для получения более точной оценки свойств генеральной совокупности приходится значительно увеличивать объем выборки.

Таким образом, вероятностная выборка — любой метод формирования выборки, предполагающий, что вероятность попадания в выборку каждого элемента совокупности известна и больше нуля.

Вероятностные методы выборки предполагают: простую случайную выборку (предполагается, что вероятность быть избранным в выборку известна и является одинаковой для всех единиц совокупности), систематическую (респонденты из списка отбираются на основе системы выбора, например каждый 10ый из списка.), кластерную (территории или зоны выступают в роли первичных выборочных единиц. Генеральная совокупность делится на ряд непересекающихся, территорий, после чего формируется случайная выборка), стратифицированную (генеральная совокупность разбивается на несколько групп, отличающихся между собой по каким либо признакам, далее респонденты выдираются из каждой группы.), пропорционально стратифицированная (если размер выборки для определённой группы пропорционален размеру группы) и оптимальное распределение.