Центр поверхности второго порядка

ЦЕНТР ПОВЕРХНОСТИ ВТОРОГО ПРЯДКА

В данной работе рассмотрено тема «центры поверхности второго прядка». Работа состоит из теоретической и практической частей. В теоретической части работы три параграфа, раскрывающих заданную тему.

Практическая часть работы содержит четыре примера по нахождению центра поверхности второго порядка.

Цель: изучить центр поверхности второго порядка.

Задача:

• 1. Уметь использовать метод преобразования при решении задач;
• 2. Уметь делать выводы;
• 3. Развить навыки решения задач по данной теме.

Определение 1. Центром поверхности второго порядка называется центр симметрии этой поверхности.

Докажем, что начало координат является центром симметрии. Для этого нужно доказать две теоремы:

Теорема 1. Пусть относительно общей декартовой (или аффинной) системы координат Oxyz, задана поверхность второго порядка общим уравнением:

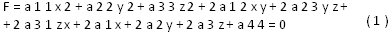
И прямая:

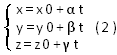
Не асимптотического направления, заданная своими параметрическими уравнениями. Для того чтобы начало координат был центром этой поверхности, необходимо и достаточно, чтобы в уравнение (1) отсутствовали члены первой степени x, y и z, т. е., чтобы a1, а2, а3 — были равны 0.

Доказательства необходимости.

Пусть начало координат является центром поверхности (1). Возьмем на этой поверхности произвольную точку М с координатами (x, y, z). Её координаты будут удовлетворять уравнению (1), а так как начало координат является центром симметрии поверхности (1), то уравнению (1) будут удовлетворять и координаты точки М' (-x, -y, -z), симметричной точке М относительно координат, т. е.:

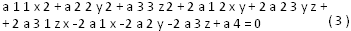
Из этого соотношения (1) находим:

a1x + a2y + a3z = 0.

Этому уравнению удовлетворяют координаты всех точек поверхности (1). Предположим, что хотя бы одно из чисел «a1, a2, a3» не равно нулю. Тогда все точки поверхности лежат в плоскости:

a1x + a2y + a3z = 0.

Это может быть тогда и только тогда, когда уравнение (1) определяет две плоскости, совпадающие с плоскостью:

a1x + a2y + a3z = 0.

На основание теоремы., левая часть уравнение (1) разлагается в произведение двух линейных относительно x, y, z множителей, одним из которых является форма:

a1x + a2y + a3z.

F = (a1x + a2y + a3z) (Ax + By + Cz + D).

Плоскость, заданная уравнением:

(Ax + By + Cz + D) = 0.

На основании сделанного выше замечание должна совпадать с плоскостью:

a1x + a2y + a3z = 0.

a1: a2: a3 = A: B: CD = 0.

И потому:

F = k (a1x + a2y + a3z) 2.

Мы приходим к противоречию с тем, что в уравнение (1) хотя бы один из коэффициентов при x, y или z в первой степени отличен от нуля.

Что и требовалось доказать.

Теорема 2. Если относительно общей системы координат поверхность второго порядка задана общим уравнением:

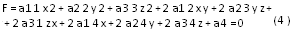
То координаты «x0, y0, z0» ее центра определяются из системы:

Причем в случае несовместимости этой системы поверхность не имеет центра.

Доказательство.

Произведем параллельный перенос данной декартовой системы координат, при котором новым началом координат будет точка О' (x0, y0, z0). Обозначая старые координаты произвольные точки М через «x, y, z», а новые ее координатычерез «x', y', z», будем иметь:

x = x' + x0, y = y' + y0, z = z' + z0.

И уравнение (1) примет вид:

F = a11x'2 + a22y'2 + a33z'2 + 2a12x'y' + 2a23y'z' + 2a31z'x' + 2 (a11×0 + a12y0 + a13z0 + a1) x' + 2 (a11×0 + a12y0 + a13z0 + a2) y' + 2 (a11×0 + a12y0 + a13z0 + a3) z' + F («x0,y0,z0») = 0.

Где:

" F («x0,y0,z0) — результат подстановки координат (x0, y0, z0) точки O' в левую часть уравнения (1).

На основании теоремы 1 точка О' (x0, y0, z0) будет центром поверхности (1) тогда и только тогда, когда:

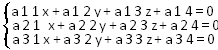
Что требовалось доказать.

Классификация поверхностей второго порядка по характеру места центров. теорема декартовый множитель Пусть поверхность второго порядка задана общим уравнением:

F = a11×2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a31zx + 2a14x + 2a24y + 2a34z + a4 = 0.

Относительно общей декартовой системы координат.

Рассмотрим матрицы:

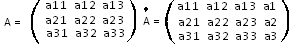
В таблице даны необходимые и достаточные признаки характера места центров поверхности, заданной уравнением:

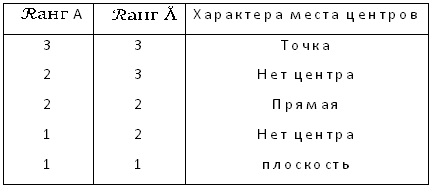
В самом деле, если каждое из уравнений (5) из является уравнением первой степени, т. е., в каждом из уравнений (5) хотя бы один из коэффициентов при x, y или z не равен нулю, то таблица сразу следует из «о» взаимном расположении трех плоскостей. Впрочем, эта таблица следует и из общей теории систем линейных уравнений.

Заключение

В данной работе были рассмотрены «центры поверхностей второго порядка». Так же были приведены примеры решений типовых задач для самостоятельной работы студента. Целью данной работы было закрепление пройденного материала.