Примеры решения задач

Здесь будут рассмотрены задачи на составление модели операции и оценку эффективности стратегии.

Составление модели операции состоит в определении множества Хстратегий ОС, множества Yнеопределенных факторов, множества Z и функции распределения (z) случайных факторов z и в определении критерия операции f (x, у, z) исходя из цели операции.

Задача 1.

Скорость движения машин в автомобильном туннеле не превышает 50 км/ч и связана с плотностью потока (количеством машин на километр дороги) Р следующим эмпирическим соотношением.

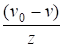
Р =,.

где v₀ = 60 км/ч, a zслучайная величина, которая в любой момент определяется отношением грузовых и легковых машин, проходящих через туннель. Известно, что величина z распределена равномерно на отрезке [0.5;1]. Регулировка движения в туннеле производится выбором скорости движения v.

За проезд по туннелю с легковой машины взимается плата денежных единиц, а с грузовой — (0<<). Цель операции состоит в получении максимальной платы за 1 час работы туннеля. Требуется составить математическую модель операции и определить оценку эффективности произвольной стратегии ОС.

Решение. Контролируемым фактором х является скорость движения v по туннелю. Множество X контролируемых факторов по условию задачи определяется соотношением.

X={x: 0×50}.

Неконтролируемым фактором является случайная величина zZ =[0.5;1] с равномерным законом распределения:

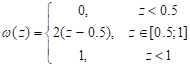
Неопределенных неконтролируемых факторов нет (Y=).

Критерием операции является количество денег, полученных в течение часа. Так как плата взимается при въезде в туннель, то для определения этой величины найдем количество С (x, z) машин, въезжающих в туннель за один час, при заданных величинах (х, z).

С (x, z)=xP=.

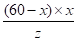
Найдем, сколько среди них грузовых и легковых. Так как.

z=,.

где — количество грузовых машин, a gколичество легковых машин, то.

g=; =.

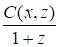
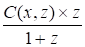
Следовательно:

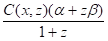
f (x, z) = .

Итак, все компоненты математической модели {X, Y, (Z,(z)), f} определены.

Оценим эффективность произвольной стратегии х. Рассмотрим только два критерия эффективности:

• 1) критерий ожидаемого значения, т. е. ОС допускает осреднение;
• 2)критерий наилучшего гарантированного результата, то есть ОС предполагает, что величина z будет реализовываться наихудшим для нее образом.

В случае 1) по формуле (11) получаем.

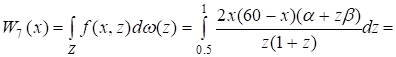
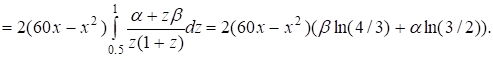
Дифференцируя по x и приравнивая к нулю, получаем, что по этой оценке лучший результат достигается при x⁰=30км/ч.

В случае 2) ОС считает z неопределенным фактором и никак не использует информацию о случайном его характере (о функции распределения вероятностей).

Полагая в формуле (3) y=z, Y=Z получаем.

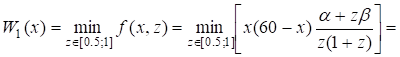
Так как функция монотонно убывает при z 0, то на отрезке [0.5; 1] она принимает минимальное значение в точке x=1, следовательно,.

.

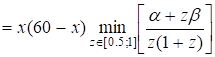
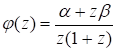
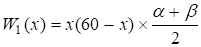
Максимум этой функции достигается в точке x⁰=30км/ч.

Задача 2.

В мэрии рассматриваются три проекта строительства теплопунктов в новом микрорайоне. Затраты по строительству, обслуживанию и развитию в соответствии с четырьмя возможными вариантами развития микрорайона.

Решение. Контролируемым фактором является выбор того или иного проекта. Обозначим x_i — выбор i-го проекта, тогда X={x₁, x₂, x₃,} - множество контролируемых факторов. Неконтролируемым фактором будет вариант развития микрорайона. Обозначим y_j — j-й вариант развития микрорайона, тогда Y={y₁, y₂, y₃, y₄} - множество неконтролируемых факторов. Так как не задано вероятностей наступления y_j, то это неопределенный фактор. Целевая функция задана в виде таблицы. Найдем решения по четырем критериям в условиях неопределенности. Напомним, что по условиям задачи ОС необходимо минимизировать затраты.

В соответствии с критерием Вальда (3).

W₁(x₁)=max{10; 15; 17; 9}=17;

W₁(x₂)=max{14; 12; 10; 16}=16;

W₁(x₃)=max{12; 13; 14; 15}=15.

Следовательно, оптимальным по этому критерию является третий проект x₃, так как при этом проекте оценка W₁(x) принимает наименьшее значение. Найдем решение по критерию Лапласа. Так как неопределенный фактор принимает четыре значения, то каждому из них припишем вероятность 0.25. В соответствии с (4) получаем.

W₂(x₁)=110.25+150.25+170.25+120.25=13.75;

W₂(x₂)=140.25+120.25+100.25+160.25=13;

W₂(x₃)=120.25+130.25+140.25+150.25=13.5.

Минимальные ожидаемые затраты получаются при x₂, следовательно, второй проект является оптимальным по критерию Лапласа.

3. Для нахождения наилучшего проекта по критерию Сэвиджа необходимо записать функцию сожаления (x, y). Так как необходимо минимизировать затраты, применим формулу (6). Функцию сожаления так же удобно записать в виде матрицы.

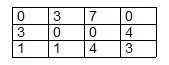
Применяя к функции сожаления критерий наилучшего гарантированного результата, получим.

W₃(x₁)=max{0; 3; 7; 0}=7;

W₃(x₂)=max{3; 0; 0; 4}=4;

W₃(x₃)=max{1; 1; 4; 3}=4.

Наименьшее значение критерия достигается на x₂, x₃. Таким образом, по критерию Сэвиджа оптимальными будут второй и третий проекты.

4. При применении критерия Гурвица ОС должна определить коэффициент [0; 1] - показатель оптимизма. Пусть =0.4. Так как в этой задаче требуется минимизировать целевую функцию, то критерий крайнего оптимизма будет задаваться как минимальное из возможных значений при данном значении x:

W₄(x₁)=min{10; 15; 17; 9}=10;

W₄(x₂)=min{14; 12; 10; 16}=10;

W₄(x₃)=min{12; 13; 14; 15}=12.

По формуле (10) получаем.

W₆(x₁)= W₄(x₁) + (1-) W₁(x₁)=0.410 + (1 — 0.4)17=14.2;

W₆(x₂)= W₄(x₂) + (1-) W₁(x₂)= 0.410 + (1 — 0.4)16=13.6;

W₆(x₃)= W₄(x₃) + (1-) W₁(x₃)= 0.412 + (1 — 0.4)15=13.8.

При выбранном значении =0.4 лучшим оказался второй проект, так как значение критерия Гурвица при x₂ наименьшее из возможных.

Задача 3.

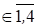
Пусть две фирмы конкурируют на рынке. Первая фирма имеет четыре стратегии, вторая — три. Если первая фирма применяет стратегию i, i= {1,2,3,4}, а вторая — стратегию j, j={1,2,3}, то первая получит выигрыш в размере f (i, j), а вторая проиграет ту же величину. Если выигрыш первой фирмы — отрицательное число, то это означает, что она проиграет такое количество условных денежных единиц, а вторая выиграет их. Функция f (i, j) задана в виде таблицы.

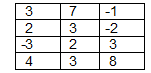
Если первая фирма применяет смешанную стратегию и допускает осреднение критерия, то оценкой эффективности () этой стратегии в случае, когда стратегия у второй фирмы является неопределенным фактором, будет наименьшее (по у) из математических ожиданий (y_j), i= выигрыша первой фирмы при фиксированном неопределенном факторе y_i;. Имеем.

(y₁)=,.

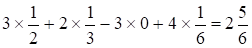
• (y₂) =
• (y₃)=

Следовательно,.

()=min.

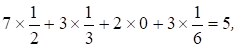
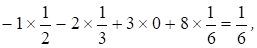
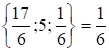
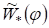
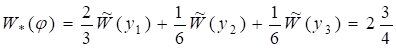
Пусть теперь и первая, и вторая фирмы применяют смешанные стратегии, и первая фирма допускает осреднение при оценке критерия. Тогда оценка стратегии будет следующей:

Задача 4.

Пусть снова две фирмы конкурируют на рынке, первая фирма имеет три стратегии, а вторая — шесть. Если первая фирма применила i-ю стратегию, а вторая — j-ю стратегию, то первая фирма получает выигрыш F⁽¹⁾(i, j), а вторая — F⁽²⁾(i, j). Эти величины могут быть разные, и необязательно противоположные. Таким образом, в отличие от предыдущей задачи вторая фирма стремится максимизировать свою функцию выигрыша, а не минимизировать функцию выигрыша первой. Пусть функции выигрышей каждой из фирм заданы в виде матриц.

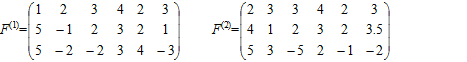
Пусть в качестве оперирующей стороны выступает первая фирма, и пусть она знает матрицу выигрышей F⁽²⁾ второй фирмы, а вторая фирма знает стратегию, выбранную первой.

Так как вторая фирма стремится максимизировать свой выигрыш, а не максимально снизить выигрыш первой фирмы, то первой фирме нецелесообразно выбирать свою стратегию из принципа гарантированного результата. Первая фирма может «вычислить» действия второй в ответ на каждое свое действие.

Если оперирующая сторона выбирает первую стратегию, то вторая фирма выбирает стратегию «4», дающую выигрыш равный 4. В этом случае выигрыш ОС будет равен также 4. Если же ОС выбирает вторую стратегию, то вторая фирма, максимизируя свой выигрыш, выберет первую. Выигрыш ОС в этом случае будет равен 5.

Пусть, наконец, ОС выберет третью стратегию, тогда вторая фирма вновь выберет первую. Выигрыш ОС будет равен 5. Итак, получены следующие оценки стратегий первой фирмы: W (1)=4, W (2)=5, W (3)=5, следовательно, ОС может выбирать либо вторую, либо третью стратегию.

Задача 5.

Решим задачу из примера 5 раздела 2.2.2 в случае, когда вероятности величин спроса на булочки неизвестны. В этом случае спрос является неопределенным фактором. Для решения воспользуемся полученной в примере таблицей значений целевой функции. Напомним, что ОС стремится максимизировать целевую функцию F (x, z).

Для оценки эффективности стратегии по критерию наилучшего гарантированного результата необходимо воспользоваться формулой (3). В соответствии с этой формулой получим следующие оценки:

W₁(x₁)=min{2400; 2400; 2400; 2400; 2400}=2400;

W₁(x₂)=min{1900; 3600; 3600; 3600; 3600}=1900;

W₁(x₃)=min{1400; 3100; 4800; 4800; 4800}=1400;

W₁(x₄)=min{900; 2600; 4300; 6000; 6000}=900;

W₁(x₅)=min{400; 2100; 3800; 5500; 7200}=400.

Наибольшее значение оценка принимает при x= x₁, следовательно, по рассматриваемому критерию необходимо закупать 100 булочек.

По критерию Лапласа в соответствии с формулой (4) получаем следующие оценки.

W₂(x₁)=(2400+2400+2400+2400+2400)1/5=2400;

W₂(x₂)=(1900+3600+3600+3600+3600)1/5=3260;

W₂(x₃)=(1400+3100+4800+4800+4800)1/5=3780;

W₂(x₄)=(900+2600+4300+6000+6000)1/5=3960;

W₂(x₅)=(400+2100+3800+5500+7200)1/5=3800.

Наибольшее значение критерия достигается при x=x₄. По критерию Лапласа нужно закупать 250 булочек.

Для определения количества закупаемых булочек по критерию Сэвиджа, вычислим функцию сожаления по формуле (5), так как задача на максимум целевой функции. Запишем функцию сожаления в виде таблицы.

Таблица 3. Значений функции сожаления (x, z).

В каждом столбце находим максимальный элемент, затем значение функции сожаления в этом столбце равно разности максимального элемента столбца и соответствующего значения целевой функции. Далее по критерию наилучшего гарантированного результата для задачи минимизации функции сожаления получаем оценки:

W₃(x₁)=max{0; 1200; 2400; 3600; 4800}=4800;

W₃(x₂)=max{500; 0; 1200; 2400; 3600}=3600;

W₃(x₃)=max{1000; 500; 0; 1200; 2400}=2400;

W₃(x₄)=max{1500; 1000; 500; 0; 1200}=1500;

W₃(x₅)=max{2000; 1500; 1000; 500; 0}=2000.

Минимальное значение критерия достигается при x = x₄, следовательно, по критерию Сэвиджа нужно закупать 250 булочек.

Найдем лучшую стратегию по критерию Гурвица при =0.2. Сначала необходимо получить оценки по критерию крайнего оптимизма (формула (9)):

W₄(x₁)=max{2400; 2400; 2400; 2400; 2400}=2400;

W₄(x₂)=max{1900; 3600; 3600; 3600; 3600}=3600;

W₄(x₃)=max{1400; 3100; 4800; 4800; 4800}=4800;

W₄(x₄)=max{900; 2600; 4300; 6000; 6000)=6000;

W₄(x₅)=max{400; 2100; 3800; 5500; 7200}=7200.

Затем по формуле (10) рассчитаем критерий Гурвица:

W₅(x₁)=0.22 400 + (1 0.2)2400=2400;

W₅(x₂)=0.23 600 + (1 0.2)1900=2240;

W₅(x₃)=0.24 800 + (1 0.2)1400=2080;

W₅(x₄)=0.26 000 + (1 0.2)900=1920;

W₅(x₅)=0.27 200 + (1 0.2)400=1760.

По критерию Гурвица при заданном значении =0.2 лучшей будет стратегия x₁ — закупать 100 булочек.