Гипотеза сплошности среды

В гидромеханике рассматриваются макроскопические движения жидкостей и газов, а также силовое взаимодействие этих сред с твердыми телами. При этом, как правило, размеры рассматриваемых объемов жидкостей, газов и твердых тел оказываются несопоставимо большими по сравнению с размерами молекул и межмолекулярными расстояниями. Это естественно, поскольку межмолекулярные расстояния в жидкостях составляют всего см.

Указанные обстоятельства позволяют ввести гипотезу сплошности изучаемой среды и заменить реальные дискретные объекты упрощенными моделями, представляющими собой материальный континуум, т. е. материальную среду, масса которой непрерывно распределена по объему. Такая идеализация упрощает реальную дискретную систему и позволяет использовать для ее описания хорошо разработанный математический аппарат исчисления бесконечно малых и теорию непрерывных функций.

Параметры, характеризующие термодинамическое состояние, покой или. движение среды, считаются при этом непрерывно изменяющимися по всему объему, занятому средой, кроме, быть может, отдельных точек, линий или поверхностей, где могут существовать разрывы.

Теоретические результаты, подученные для гипотетической сплошной среды, тем лучше совпадут с результатами наблюдений, чем полнее и точнее учтены в ней свойства реальных жидкостей и газов. К сожалению, идеализацию среды во многих случаях не удается ограничить только допущением ее сплошности. Сложность изучаемых явлений заставляет отказываться от учета и некоторых других свойств реальных сред. В зависимости от тех свойств, которые приписываются гипотетической сплошной среде, получают различные ее модели.

Гипотеза сплошности среды означает, что всякий малый элемент объема жидкости считается все-таки настолько большим, что содержит еще очень большое число молекул. Соответственно этому, когда мы будем говорить о бесконечно малых элементах объема, то всегда при этом будем подразумевать «физически» бесконечно малый объем, т. е. объем достаточно малый по сравнению с объемом жидкости, но большой по сравнению с молекулярными расстояниями.

Согласно гипотезе сплошности масса среды распределена в объеме непрерывно и в общем неравномерно. Основной динамической характеристикой среды является плотность распределения массы по объему или просто плотность среды.

Плотность среды в произвольной точке А определяется соотношением.

(9).

где — масса, заключенная в малом объеме, включающем точку А; предел берется при стягивании объема к этой точке.

Наряду с плотностью в рассмотрение вводится понятие удельного объема, который представляет собой объем, содержащий единицу массы:

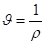
. (10).

Плотность среды может изменятся от точки к точке и в данной точке со временем, т. е.

(11).

Аналогично для давления имеем . Как известно, по двум термодинамическим величинам с помощью уравнения состояния вещества могут быть определены все термодинамические величины. Таким образом, задание пяти величин: трех компонентов скорости , давления и плотности полностью определяет состояние движущейся жидкости. Подчеркнем, что есть скорость жидкости в каждой данной точке х, у, z пространства в момент времени t.

Однако эта функциональная связь не является непосредственной, так как плотность жидкостей и газов определяется фактически значениями термодинамических параметров состояния (р и Т), которые при движении среды зависят от координат (х, у, z) и времени (t).

Математическое описание движения жидкой среды общими дифференциальными уравнениями, учитывающими все физические свойства, присущие этой среде, оказывается весьма сложной задачей. Если даже ограничится учетом только текучести, вязкости и сжимаемости, то и тогда уравнения движения, выражающие основные законы механики, оказываются настолько сложными, что пока не удалось разработать общих аналитических методов их решения. Применение численных методов интегрирования таких уравнений на базе современных ЭВМ также связано со значительными трудностями. В гидромеханике поэтому широко используют различные упрощенные модели среды и отдельных явлений.

Под моделью реальной среды понимают такую гипотетическую среду, в которой учтены только некоторые из физических свойств, существенные для определенного круга явлений и технических задач. Другие малосущественные свойства среды в модели игнорируются.

Одной из основных в гидромеханике является модель несжимаемой идеальной (или невязкой) жидкости. Так называется гипотетическая сплошная среда, обладающая текучестью, лишенная вязкости и полностью несжимаемая. Эта модель является объектом исследования в разделе гидромеханики «Теория идеальной несжимаемой жидкости». Игнорирование свойств вязкости и сжимаемости сильно упрощает математическое описание движения жидкости и позволяет получить многие решения в конечном замкнутом виде. Несмотря на значительную степень идеализации среды, теория несжимаемой невязкой жидкости дает ряд не только качественно, но и количественно подтверждаемых опытом результатов, полезных для практических приложений. Но не менее существенное значение этой теории состоит в том, что она является базой для других моделей, более полно учитывающих свойства реальных сред. Следует, однако, подчеркнуть, что пренебрежение вязкостью является весьма сильной степенью идеализации, поэтому теория идеальной несжимаемой жидкости может приводит к результатам, резко расходящимся с опытом.

Более полно свойства реальной жидкости учитываются в модели вязкой несжимаемой жидкости, которая представляет собой среду, обладающую текучестью и вязкостью, но абсолютно несжимаемую. Теория вязкой несжимаемой жидкости лишь в ограниченном числе случаев с простейшими граничными условиями позволяет получить точные решения полных уравнений движения. Наибольшее значение в этой теории имеют приближенные уравнения и их решения. Такие уравнения получают путем отбрасывания в полных уравнениях движения тех членов, которые мало влияют на соответствие теоретических решений опыту. Решения приближенных уравнений могут быть как точными, так и приближенными.

Как известно, капельные жидкости являются малосжимаемыми средами, поэтому для широкого круга теоретических и прикладных задач пренебрежение сжимаемостью является вполне допустимой идеализацией и мало влияет на вид получаемых решений и степень совпадения теоретических результатов с данными измерений. Но все же существуют случаи движения жидкостей, которые нельзя достаточно достоверно описать, если не учесть сжимаемость.