Равновесие статических сил в плоском механизме

Равновесие статических сил в плоском механизме

Для одного из заданных положений плоского механизма (рис. 1), находящегося в равновесии, составить уравнения равновесия с учётом сил тяжести звеньев, уравновешивающего момента Мур. = Мдв. = 0,80 Н? м, приложенного к ведущему звену АВ, и технологической силы Qт, приложенной в точке К, и определить величину (Qт) и направление (?) технологической силы Qт.

Значения сил тяжести примем равными:

Р1 = 0,50 Н; Р2 = 3,00 Н; Р3,4 = 4,00 Н; Р5 = 2,00 Н.

Длины звеньев заданные в мм:

L1 = 40 мм; L2 = 140 мм; L3 = 90 мм; L4 = 60 мм.

Расстояние от точки, А до точки К, lк = 55 мм.

Начальный угол поворота ведущего звена АВ ?1 = 60О.

Решение Применим метод размыкания кинематической цепи, который базируется на условном размыкании некоторых кинематических пар с тем, чтобы кинематическая цепь приобрела структуру «дерево». Метод применим для всего механизма в целом и для отдельных структурных групп. При этом уравнения равновесия составляются в форме уравнений моментов относительно осей шарниров, и уравнений проекций сил на оси, соответствующие линейным координатам.

Условно разомкнем механизм в шарнирах D и H для того, чтобы кинематическая цепь приобрела структуру «дерево» (рис. 2), а действие связей заменим соответствующими проекциями реакций.

Изобразим в масштабе 1:1 получившуюся разомкнутую кинематическую цепь (рис. 3).

Так как схема построена в масштабе 1:1, то измерим координаты характерных точек механизма, вычислим углы поворота звеньев и сведём эти данные в таблицу 1.

кинематический цепь равновесие сила.

Таблица 1.

Рассмотрим отдельно от кинематической цепи звено 3, на которое действует только одна внешняя сила Р3 в точке «3», в середине звена (рис. 4).

Составим уравнение суммы моментов сил, приложенных к звену 3, при условии его равновесия.

Отсюда.

Для определения силы реакции R04, и проекций QTx и QTy уравновешивающей технологической силы QТ составим систему уравнений равновесия открытой кинематической цепи в виде суммы моментов относительно шарниров С, В и А.

(2).

Примем размерность данных и вычисляемых величин в Н и мм.

Мдв =0,800 кН? мм = 800 Н? мм Заменим проекции R04x и R04y силы реакции R04 самой этой силой R04.

Примем к сведению, что заданные силы Р3 = Р4 = Р = 4,00 Н и найденная сила реакции R03 = P3/2 = P/2 = 2,00 Н Подставим эти данные и данные координат механизма из таблицы 1 в уравнения (1), (2) и (3).

Из уравнения (1) найдём силу реакции R04.

Из уравнений (2) и (3) найдём проекции технологической силы QT.

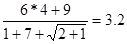
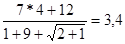
Получили систему двух уравнений с двумя неизвестными.

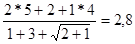
Разделим первое уравнение на 81, а второе — на 61 и получим.

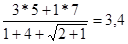
Просуммируем оба уравнения.

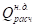
Определим угол направления силы QT.

Модуль силы QT.

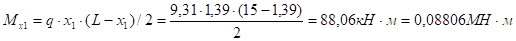
Ответ:; .

Использованная литература

1. Ю. А. Семенов, Н. С. Семенова. Статика механизмов. Теория механизмов и машин. 2006, № 2, том 4.