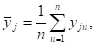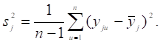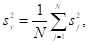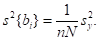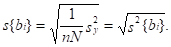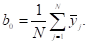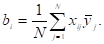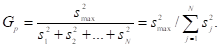Помощь в написании студенческих работ
Антистрессовый сервис

Расчёт коэффициентов уравнения регрессии и выделение значимых коэффициентов

Реферат: Расчёт коэффициентов уравнения регрессии и выделение значимых коэффициентов
РефератПомощь в написанииУзнать стоимостьмоей работы

Для определения коэффициентов уравнения регрессии и выделения значимых коэффициентов выполняем следующие расчёты (все расчёты здесь и далее выполнены в электронных таблицах «Microsoft Excel 2003» из пакета «Microsoft Office 2003 (SP2)»). Находим доверительный интервал bi по формуле где t — табличное. значение критерия (Коэффициент Стьюдента) при принятом уровне значимости б = 0,05 и числе… Читать ещё >

Расчёт коэффициентов уравнения регрессии и выделение значимых коэффициентов (реферат, курсовая, диплом, контрольная)

Для определения коэффициентов уравнения регрессии и выделения значимых коэффициентов выполняем следующие расчёты (все расчёты здесь и далее выполнены в электронных таблицах «Microsoft Excel 2003» из пакета «Microsoft Office 2003 (SP2)»).

1) По формуле рассчитываем среднее значение отклика

,.

,.

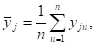
где n — количество дублирований опытов (n = 3).

2) По формуле рассчитываем среднее значение квадрата отклонений случайной величины от ее среднего значения (построчную дисперсию) опытов согласно матрице планирования.

Расчёт коэффициентов уравнения регрессии и выделение значимых коэффициентов.

3) Вычисляем дисперсию воспроизводимости (общую дисперсию):

Расчёт коэффициентов уравнения регрессии и выделение значимых коэффициентов.

.

где N — число экспериментов (N = 16).

4) Находим дисперсию i-го коэффициента по зависимости:

Расчёт коэффициентов уравнения регрессии и выделение значимых коэффициентов.

5) и ошибку эксперимента:

Расчёт коэффициентов уравнения регрессии и выделение значимых коэффициентов.

6) Рассчитываем коэффициенты уравнения регрессии. Свободный член вычисляем по зависимости:

Расчёт коэффициентов уравнения регрессии и выделение значимых коэффициентов.

.

7) Коэффициенты регрессии, характеризующие линейные эффекты, вычисляем по зависимости:

Расчёт коэффициентов уравнения регрессии и выделение значимых коэффициентов.

На основании полученных расчётов имеем следующие значения коэффициентов регрессии (Табл. 2), по которым записываем уравнение регрессии:

= 121,404−0,063x1-0,296x2-0,379x3-1,475x4-0,037x12-0,254x13— -0,092x14+0,371x23-0,242x24-0,492x34-0,046x123+0,092x134-0,392x234-0,117x124+0,092x134—0,017x1234

Таблица 2.

№ опыта Факторы.

X0

X1

X2

X3

X4

X12

X13

X14

X23

X24

X34

X123

X134

X234

X124

X134

X1234

s2j

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

121,00.

0,250.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

120,50.

0,250.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

119,83.

0,083.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

118,83.

0,083.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

118,50.

0,250.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

119,50.

0,250.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

120,50.

0,250.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

120,77.

0,063.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

121,60.

0,280.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

121,30.

0,490.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

122,43.

0,163.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

122,70.

0,130.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

122,93.

0,093.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

123,53.

0,253.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

— 1.

123,93.

0,163.

124,60.

0,280.

bi

121,404.

0,063.

0,296.

0,379.

1,475.

— 0,037.

0,254.

0,092.

0,371.

0,242.

0,492.

— 0,046.

— 0,092.

— 0,392.

0,117.

— 0,092.

— 0,017.

s2y = 0,208.

s2{bi} = 0,0043.

s{bi} = 0,0656.

8) Находим доверительный интервал bi по формуле где t — табличное. значение критерия (Коэффициент Стьюдента) при принятом уровне значимости б = 0,05 и числе степеней свободы f = 2, с которым определялась дисперсия, tф = 4,3;

Дbi = 0,2833.

Находим максимальное значение s2y max.

s2y max = 0,490.

Проверяем однородность ряда дисперсий с помощью G-критерия Кохрена, представляющего собой отношение максимальной дисперсии к сумме всех дисперсий:

Расчёт коэффициентов уравнения регрессии и выделение значимых коэффициентов.

Gp = 0,1470.

Табличное значение при 5% уровне значимости при N = 16 и (n — 1) = 2:

Gтабл = 0,3346.

Gp < Gтабл, следовательно, дисперсии однородны.

Исключаем незначимые факторы и записываем новое уравнение регрессии с учётом только значимых факторов, удовлетворяющих условию т. е. факторов, попадающих в доверительный интервал:

= 121,404−0,296×2−0,379×3−1,475×4−0,371×23−0,492×34−0,392×234.

Показать весь текст
Заполнить форму текущей работой

Сессия? Спокойно!