Парный регрессионный анализ взаимодействия уровня безработицы и ввп в российской федерации

Построение модели парной регрессии

Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.

Линейная регрессия сводится к нахождению уравнения вида:

или.

Уравнение позволяет по заданным значениям фактора x иметь теоретические значения результативного признака подстановкой в него фактических значений фактора x.

Расчет параметров уравнения линейной регрессии.

Таблица 1. Исходные данные.

Примечание: Данные граф 3, 4 взяты из статистики Госкомстат и Статинфо.

С помощью табличного процессора Excel, вычислим коэффициенты модели парной регрессии и проверим значимость уравнения регрессии (таблица 2).

Таблица 2. Уравнение регрессии y = a + bx.

Примечание: режим регрессия, пакет анализа Microsoft Excel.

С помощью СТЬЮДРАСПОБР tкр, tкр= 2,144. Сравнивая значения tстатистики с рассчитанным критерием, получаем: значение всех переменных (X= -4,48) по модулю больше чем tкр= 2,144, а значит, фактор значим. Итоговое уравнение имеет вид:

Y= 9,14 695 — 0,00006X.

Коэффициент этого уравнения показывает, что снижение ВВП способствует снижению уровня безработицы.

Далее следует выявить значимость выбранного фактора. Для этого следует определить адекватность построенной модели.

Рассмотрим коэффициент детерминации .

Данный коэффициент показывает долю полной вариации объясняемой переменной, она детерминирована объясняющими переменными. Для полученной нами регрессии коэффициент детерминации это означает что модель примерно на 86% раскрывает степень влияния фактора, то есть модель имеет высокую значимость.

Коэффициент множественной регрессии R=0,93, он показывает тесноту связи зависимой переменной (уровень безработицы) с объясняющим фактором, входящим в модель регрессии.

Далее оценим адекватность модели по F-критерию Фишера.

Для этого воспользуемся функцией FРАСПОБР в программе Microsoft Excel. Получаем, =4,75.

Получаем что табличное значение меньше, следовательно, модель адекватна и пригодна для использования.

Найдем среднюю ошибку аппроксимации.

Средняя ошибка аппроксимации — это среднее отклонение расчетных значений от фактических.

Для этого воспользуемся остатками модели Таблица 3. Вывод остатков.

Примечание: режим регрессия, пакет анализа Microsoft Excel.

Таблица 4. Расчетная таблица для вычисления средней ошибки аппроксимации.

t.	Уровень безработицы, %.	ВВП, в млрд.руб.
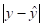Y.	Х.
	10,6.	7305,6.	8,739 816.	1,9.	1,9.	0,179 245.
	9,0.	8943,6.	8,648 535.	0,4.	0,4.	0,44 444.
	7,9.	10 830,5.	8,543 376.	— 0,6.	0,6.	0,55 949.
	8,2.	13 208,2.	8,410 869.	0,2.	0,2.	0,2 439.
	7,8.	17 027,2.	8,198 041.	— 0,4.	0,4.	0,51 282.
	7,1.	21 609,8.	7,942 657.	— 0,8.	0,8.	0,12 676.
	7,1.	26 917,2.	7,646 877.	— 0,5.	0,5.	0,70 423.
	6,0.	33 247,5.	7,294 093.	— 1,3.	1,3.	0,16 667.
	6,2.	41 276,8.	6,846 624.	— 0,6.	0,6.	0,96 774.
	8,3.	38 807,2.	6,984 255.	1,3.	1,3.	0,156 627.
	7,3.	46 308,5.	6,566 211.	0,7.	0,7.	0,9 589.
	6,5.	55 644,0.	6,45 951.	0,5.	0,5.	0,76 923.
	5,5.	61 810,8.	5,702 279.	— 0,2.	0,2.	0,36 364.
	5,5.	66 689,1.	5,430 417.	0,1.	0,1.	0,18 182.

Примечание: данные графы 2, 3 взяты из статистики Госкомстат и Статинфо; данные графы 4 предсказанное Y из таблицы 3; данные графы 5 получены путем вычитания из графы 2 графу 5; данные графы 6 это данные графы 5 по модулю; данные графы 7 получены путем деления графы 6 на графу 2.

Таким образом, по формуле (2.22), получаем.

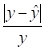
Поскольку ошибка меньше 10%, то можно говорить о хорошем подборе модели к исходным данным.

Проанализируем уравнение регрессии полностью, то есть проверим выполняются ли предпосылки метода наименьших квадратов (МНК).

Исследование остатков предполагает проверку присутствие следующих пяти предпосылок МНК:

• § случайный характер остатков;
• § нулевая средняя величина остатков, не зависящая от ;
• § гомоскедастичность — дисперсия каждого отклонения одинакова для всех значений

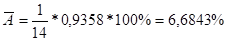
• § отсутствие автокорреляции остатков — значения распределены независимо друг от друга;
• § остатки подчинены нормальному распределению.

Для анализа используем таблицу 3.

Остатки исследуемого тренда образуют S= 5 серии, уровень значимости равен 0,05. В таблице «Критерии значения для количества серий» находим критические значения (Таблицы, стр. 354). Получаем, что, следовательно, аналитическая форма модели выбрана удачно.

Определим случайный характер остатков.

Построим график отклонений фактических значений от теоретических значений признака.

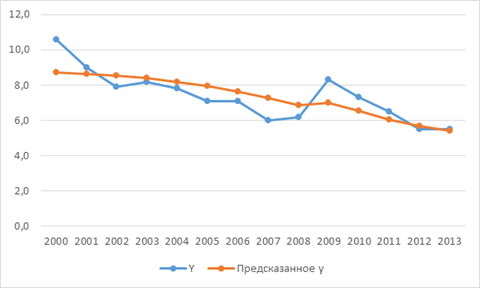
Рисунок 3.1. Фактические и теоретические значения уровня безработицы в Российской Федерации с 2000 по 2013 гг.

На рис. 3.1 показано как построенная модель парной регрессии аппроксимирует уровень безработицы в Российской Федерации с 2000 по 2013 года.

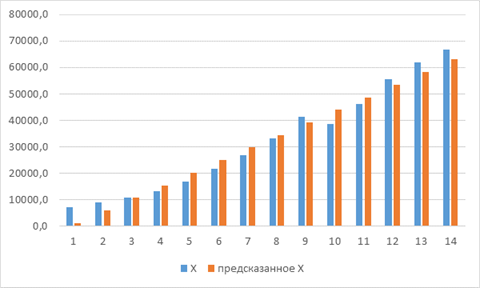
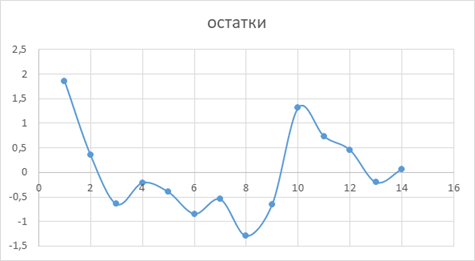
Рисунок 3.2 График остатков.

На рисунке 3.2 показан график остатков, получена горизонтальная полоса, которая показывает, что остатки представляют собой случайные величины и применение МНК оправдано.

Далее нужно определить присутствие зависимости остатков от. Рассмотрим нулевую величину остатков, которая не зависит от. В качестве критерия рассмотрим статистику:

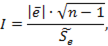
где — среднее арифметическое остатков — стандартное отклонение.

Рассчитаем критерий t-теста Стьюдента для m=n-1, m=14−1=13 степеней свободы и для уровня значимости 0,05. Определим с помощью функции СТЬЮДРАСПОБР в Microsoft Excel. Если I*I, то математическое ожидание случайных отклонений несущественно отличается от 0, то есть отклонение признается несмещенным. В противно случае мат ожидание отличается от 0, значит отклонение признается смещенным. Так как модель линейная и построена по МНК, то значит и I тоже равно 0. Получились такие результаты: I*= 2,160, значит I* является критическим значением. Получается, что I*I, то есть отклонение несмещенное.

Далее проверим отсутствие автокорреляции остатков с помощью критерия Дарбина — Уотсона в нашем случае.

Таблица 5. Вспомогательная таблица для вычисления критерия Дарбина-Уотсона.

Примечание: данные графы 2 взяты из статистики Госкомстат и Статинфо; данные графы 2 это предсказанное Y взяты из таблицы 3; данные графы 4 остатки взяты из таблицы 3; данные графы 5 получены путем вычитания из последующего значения предыдущего; данные графы 6 получены путем возведения в квадрат графы 5; данные графы 7 получены путем возведения в квадрат графы 4.

Таким образом, получаем из (2.27), что .

Из таблицы «Значения статистики Дарбина-Уотсона» [Елисеева стр. 566] определим критические значения критерия Дарбина-Уотсона 1,05 и для заданного числа наблюдений 14 и числа независимых переменных модели равного 1, уровня значимости б=0,05.

Получаем, что 1,34<0,97<-0,34, это говорит о том, что нет оснований отклонять гипотезу об отсутствии автокорреляции в остатках.

Проверим наличие гетероскедастичности в остатках регрессии с помощью рангового коэффициента Спирмена. Суть этой проверки заключается в том, что в случае гетероскедастичности абсолютные остатки коррелированы со значением фактора. В таблице 6 показан расчет рангового коэффициента Спирмена.

Таблица 6. Расчет рангового коэффициента корреляции Спирмена.

Примечание: данные графы 2 получены путем ранжирования от большего к меньшему графы 4 таблицы 1; данные графы 3 получены путем ранжирования значений, взятых по модулю от меньшего к большему графы 4 таблицы 2.

После присвоения х рангов (табл. 6), нужно найти абсолютные разности между ними, возвести их в квадрат и просуммировать, затем полученные значения подставить в формулу (2.25) для расчета коэффициента ранговой корреляции Спирмена по каждому фактору.

Таблица 7. Расчет коэффициента ранговой корреляции Спирмена.

Примечание: данные графы 2 получены путем вычитания из графы 3 таблицы 6 графы 2 таблицы 6; данные графы 3 получены путем возведения в квадрат графы 2.

Коэффициент ранговой корреляции Спирмена для Х равен:

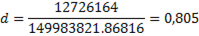
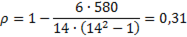
Статистическую значимость коэффициента можно определить с помощью t-критерия (2.26).

Таким образом, получаем:

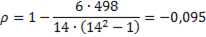
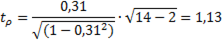
Далее сравним эту величину с табличной величиной, рассчитанной с помощью функции в Microsoft Exel СТЬЮДРАСПОБР при б=0,05 и числе степеней свободы n=2=14−2=12;

Получается что,, тогда принимается гипотеза об отсутствии гетероскедастичности остатков.

Далее исследуем остатки на наличие нормальности распределения с помощью теста Шапиро-Уилка.

Таблица 8. Расчетная таблица для вычисления статистики W.

Примечание: данные графы 2 — это остатки из табл.2, данные графы 3 получены путем ранжирования от меньшего к большему графы 2, данные графы 4 получены путем возведения квадрат графы 3, данные графы 5 взяты из табл. [http://www.machinelearning.ru/wiki/index.php?title], данные графы 6 получены путем вычитания соответствующего, но номеру значения из графы 3, данные графы 7 получены путем умножения графы5 на графу 6.

Так как.

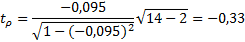
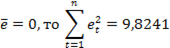
Из таблицы выбираем критическое значение W*, для n=14 и уровня значимости б = 0,05, W*= 0,874. Так как W>W*, то можно утверждать о том, что распределение случайных отклонений нормальное. Все предпосылки МНК выполнены, что говорит о качестве полученных оценок параметров эконометрической модели.

Рассчитаем средний коэффициент эластичности по формуле (2.10):

Таким образом, ВВП является статистически значимым фактором, оказывающим влияние на уровень безработицы в Российской Федерации.