Непрерывные функции. 
Разрывные и непрерывные функции

Функции, не имеющие производной. Правая и левая производные

Введем два новых определения. Если? стремится к нулю, принимая только положительные значения, то предел отношения.

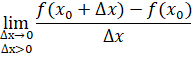
(если он существует) называется производной справа или правой производной от функции ѓ() в точке ?, а если? стремится к нулю, принимая только отрицательные значения, то предел этого же отношения (если он существует) есть производная слева или левая производная. Производную справа обозначают символом, а производную слева — символом .

Если производная справа и производная слева равны между собой, то функция, очевидно, имеет производную в точке ₀ в обычном смысле слова.

Наиболее простые примеры функций, имеющих в некоторой точке правую и левую производные, не совпадающие между собой, дают нам функции, графики которых представляют собой ломаные линии.

В самом деле, пусть ₁, ₂, …, _к, …, _s — некоторое число различных точек на оси. Построим ломаную так, чтобы ее вершины имели абсциссы, равные х₁, ₂, …, _к, …, _s (рис. 12). Функция ѓ(), графиком которой является эта ломаная *), не имеет производной в точках ₁, ₂, …, _к, …, _s .

*) Очевидно, каждая прямая, перпендикулярная к оси Ох, пересекает ломаную не более чем в одной точке, и ломаная представляет собой график некоторой однозначной функции.

Для того чтобы это доказать, рассмотрим какую-нибудь точку Q с абсциссой _к. График функции в окрестности этой точки имеет вид, изображенный на рис. 13.

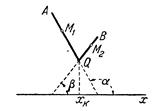
Рис. 13.

Для всякой прямой линии секущая в некоторой ее точке, а, следовательно, и касательная (как предельное положение этой секущей), совпадают с самой прямой; значит, угол секущей, а, следовательно, и касательной к прямой с осью, есть тот же самый, что и угол самой прямой с осью х.

Обозначим угол прямой AQ с осью через б и угол прямой QB с осью через в. Проводим секущую через точку Q и точки М₁ и М₂, находящиеся слева и справа от Q. Левая секущая совпадает с прямой AQ, а правая — с прямой QB.

Ясно, что если рассматривать Q как точку прикосновения, то у секущей будет два предельных положения, или, как иногда говорят, кривая в этой точке будет иметь правую касательную, совпадающую с прямой QB, и левую касательную, совпадающую с прямой AQ. Угол между осью и левой касательной, очевидно, равен б, а угол между осью и правой касательной равен в. Так как б и в различны, то и.

tg б? tg в.

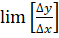
Таким образом, в точке Q у нашей линии нет определенной касательной, а так как производная равна тангенсу угла касательной с осью, то производная слева не равна производной справа и не существует в точке Q.

Рассмотрим еще один пример функций с различными производными слева и справа. Пусть требуется найти производную от функции.

y=ѓ()=².

Функция, очевидно, определена в промежутке -1??+1. График ее изображен на рис. 14. Кривая заканчивается в точках М (-1, +1) и N (+1, +1), так как для ||>1 функция не определена.

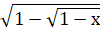
Находим производную в точке х:

Полагая х=0, находим значение производной в точке О (0, 0):

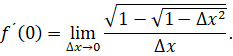
Чтобы найти предел, мы умножаем и числитель, и знаменатель на.

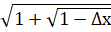
²:

Так как рассматривается арифметическое (положительное) значение квадратного корня, то ²=?, если? х>0, но ²=-?, если ?<0.

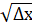
Следовательно, если ?>0, то.

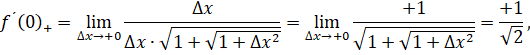
а если ?<0, то.

Мы видим, что производная слева не равна производной справа, а потому наша функция не имеет производной. Точка (0, 0) есть угловая точка, в которой кривая не имеет определенной касательной.

Возможны случаи, что отношение не имеет определенного предела ни тогда, когда ?>0, принимая только положительные значения, ни тогда, когда ?>0, принимая только отрицательные значения. В этом случае функция не будет иметь в данной точке производной ни в обычном смысле слова, ни в правой, ни в левой.

Как пример такого случая рассмотрим функцию =ѓ(), определенную двумя равенствами:

= sin при ?0,.

= ѓ()=0 при =0,.

Вычислим производную этой функции при х=0. Составим приращение ?:

?= ѓ(+?) — ѓ();

при =0 будем иметь:

[?]_х=0= ѓ(?) — ѓ(0).

Так как.

ѓ()= sin, ѓ(?) =? sin ,.

и согласно принятому условию ѓ(0)=0, то.

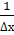
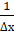
[?]_х=0= [ѓ(?)]_x=0=? sin ,.

а потому,.

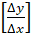
_x=0= sin .

Итак, значение производной в точке (0, 0) должно быть равным.

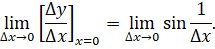
Но так как sin при ?>0 не стремится ни к какому пределу, то при =0 не существует ни левой, ни правой касательной.