Примеры доказательства пятого постулата

В.Я. Буняковский делит доказательства постулата о параллельных на четыре категории. Обратимся к доказательствам, которые входят в классификацию В. Я. Буняковского.

• 1 категоия: Доказательства, в которых содержатся прямые ошибки.
• 2 категория: Первую и основную категорию доказательств постулата о параллельных линиях по Буняковскому образуют те, которые непосредственно или после ряда предвари тельных построений явно или неявно делают допущение, эквивалентное постулату Евклида. К этой категории принадлежит значительное большинство доказательств постулата.
• 3 категория: К третьей категории Буняковский относит доказательства, основанные на так называемом принципе однородности. Этот принцип заключается в том, что отрезок никогда не может определяться углами. Так, например, в треугольнике сторона с не может быть функцией его углов, т. е. не может иметь, место равенство вида:

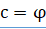
(A, B, C).

Доказательства Валлиса

Первый пример В 1663 г. в Оксфордском университете профессор Дж. Валлис прочел лекцию, содержавшую доказательство постулата о параллельных.

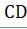
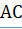
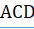
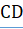
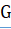
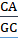
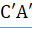
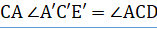
Нужно доказать, что перпендикуляр и наклонная к секущей непременно пересекаются со стороны острого угла Опустим из точки луча на прямую перпендикуляр, который упадёт в точку со стороны острого угла. Построим треугольник, подобный треугольнику при отношении сходственных сторон, равном, тогда сторона будет равна. Если приложим треугольник C’A’E' к прямой АС с надлежащей стороны так, чтобы сторона его C’A' совпала с отрезком АС, то прямые A E' и C E' пойдут соответственно по АВ и СD, и точка E' упадет в точку Е, в которой перпендикуляр АВ пересечется с наклонной СF.

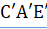
Рассуждение кажется безукоризненным, но оно предполагает, что каждому треугольнику соответствует подобный ему треугольник при любом отношении подобия. Но такое допущение даже шире постулата Евклида, т.к. из существования подобных треугольников следует постулат Евклида и вся его геометрия.

Второй пример

«Пусть АВ и CD будут прямые, пересекающие неограниченную прямую ACF и образующие с нею по одну сторону внутренние углы ВАС и DCА, которые вместе составляют меньше двух прямых.

Я утверждаю, что прямые АВ и CD при неограниченном продолжении встречаются и именно с той стороны прямой AF, с которой лежат эти два угла.

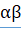
В самом деле, представим себе, что прямая АС, расположенная между ними на неограниченной прямой ACF, прямолинейно по ней передвигается. Положим, далее, что прямая АВ, опирающаяся на АС, движется вместе с этим отрезком, сохраняя угол ВАС, до тех пор пока, т. е. движущаяся прямая АВ, встретит прямую CD в некоторой точке. Тогда есть треугольник, и существует другой подобный ему треугольник любой величины. Поэтому на отрезке СА (как на основании) можно построить треугольник, подобный треугольнику, с основанием СА. Пусть это выполнено и PCА есть этот треугольник".

Авторы доказательства постулата о параллельных линиях естественно стараются обеспечить себя от возможных возражений; при этом они очень часто входят в пространные рассуждения о совершенно тривиальных вещах, которыми правильность вывода совершенно не нарушается. Мы опускаем такого рода тривиальные соображения Валлиса и воспроизводим продолжение доказательства .Так как PCА есть треугольник, то стороны СР и АР (по определению треугольника) встречаются в точке Р; а так как.

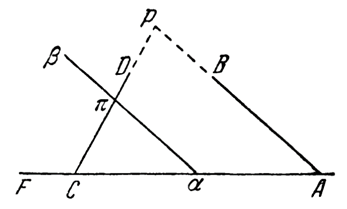
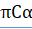
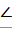
треугольник РСА подобен треугольнику (по построению), токаждый угол одного треугольника равен соответствующему углу другого треугольника (согласно определению подобных прямолинейных фигур). В соответствии с этим РСА равен углу, т. е. DCA, и прямая СР лежит на продолжении прямой CD ибо, если бы прямая CD лежала по одну или другую сторону от (СP), то РСА был бы больше или меньше DCА, между тем как равенство их доказано.

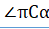
Точно так же угол РАС равен углу. Но тому же, т. е., равен BAF или ВАС, а потому ВАС равен РАС. Следовательно, прямая АР лежит на продолжении прямой АВ (если бы она лежала по одну или другую сторону ее, то ВАС и РАС не были бы равны, между тем как равенство их доказано).

Таким образом, прямая АР совпадает с продолжением прямой АВ. Совершенно так же СР и продолжение CD образуют прямую. Но, как уже было показано, АР и СР встречаются в точке Р; поэтому встречаются и продолжения прямых АВ и CD и именно в этой точке Р, т. е. с той стороны прямой ACF, с которой лежат два угла, составляющие меньше двух прямых, что и требовалось доказать.

Это доказательство я провел по самым строгим правилам, по образцу Евклида, чтоб даже и строгий судья не мог мне сделать упрека в его неполноценности. Однако, я совершенно не порицаю Евклида за то, что он не дал доказательства: напротив, я не имел бы ничего против того, чтобы он ввел еще большее число недоказанных постулатов, например, если бы он (вместе с Архимедом) постулировал, что прямая линия короче всех линий, проходящих между теми же концами; ему бы тогда не пришлось излагать 19 предложений, раньше чем доказать, что две стороны треугольника, вместе взятые, больше третьей, и многое другое, что само по себе очевидно".

Существенная заслуга Валлиса заключается в том, что он четко формулирует то допущение, которое в его рассуждении заменяет постулат о параллельных линиях. В отличие от многих других авторов, которые делают то или иное допущение молчаливо, скрывая это от себя и от читателя, Валлис высказывает убеждение, что без специального постулата учение о параллельных линиях обойтись не может. Валлис обнаружил, что допущение существования подобных фигур эквивалентно постулату Евклида; в этом — значение его рассуждений. Саккери, анализируя доказательство Валлиса, уточнил этот результат; он показал, что достаточно принять существование двух подобных неравных треугольников, т. е. одной пары треугольников, которые имеют соответственно равные углы, но неравные стороны, чтобы доказать евклидов постулат.