Методика решения задач на построение

Характеристика задач на построение

Задача на построение

Задача на построение состоит в том, что требуется построить наперёд заданными инструментами некоторую фигуру, если дана некоторая другая фигура и указаны некоторые соотношения между элементами искомой фигуры и элементами данной фигуры.

Каждая фигура, удовлетворяющая условиям задачи, называется решением этой задачи.

Найти решение задачи на построение — значит свести её к конечному числу основных построений, т. е. указать конечную последовательность основных построений, после выполнения которых, искомая фигура будет уже считаться построенной в силу принятых аксиом конструктивной геометрии. Перечень допустимых основных построений и ход решения существенно зависит от того, какие именно инструменты употребляются для построений.

В качестве примера рассмотрим следующую задачу: построить середину отрезка, заданного своими концами, А и В.

Найдем решение этой задачи с помощью различных инструментов.

1. Циркулем и линейкой (рис. 24).

Строим последовательно:

• 1) Прямую АВ;
• 2) Окружность щ (А, АВ);
• 3) Окружность щ (В, ВА);
• 4) Общие точки М и N окружностей щ и щ;
• 5) Прямую МN;
• 6) Общую точку О прямых АВ и МN.

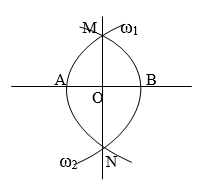
Рис. 24.

Легко убедиться, что АО=ОВ, т. е. точка О искомая.

2. Циркулем (рис. 25).

Строим последовательно:

• 1) Окружность щ (В, ВА);
• 2) Окружность щ₁ (А, АВ);
• 3) Общую точку окружностей щ и щ;
• 4) Окружность щ₂ (С, CА);
• 5) Общую точку D окружностей щ и щ₂, отличную от точки А;
• 6) Окружность щ₃ (D, DB);
• 7) Общую точку Е окружностей щ и щ₃.

Заметим, что точки А, В, Е расположены на одной прямой, причем отличную от А. АЕ=2АВ.

Строим далее:

• 8) Окружность щ₄ (Е, ЕА);
• 9) Общие точки М и N окружностей щ₁ и щ_4;
• 10) Окружность щ₅ (М, МА);
• 11) Окружность щ₆ (N, NА);
• 13) Общую точку Х окружностей щ₅ и щ₆, отличную от С.

Нетрудно усмотреть, что точка Х расположена на прямой АВ.

Кроме того, треугольник АМХ подобен треугольнику АЕМ, т.к. они равнобедренные и имеют общий угол МАЕ при основаниях.

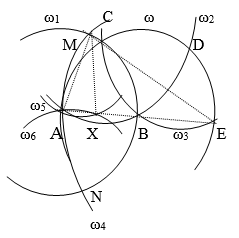
Рис. 25.

Поэтому, АХ: АМ=АМ:АЕ или АХ: АВ=АВ:2АВ,.

АХ=АВ и, значит, точка Х искомая.

3. Двусторонней линейкой (рис. 26).

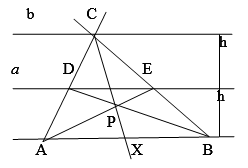
Рис. 26.

Строим последовательно:

• 1) Прямую АВ
• 2) Прямую a, параллельную АВ и проходящую на расстоянии h от неё;
• 3) Прямую b, параллельную a, отстоящую от неё на расстоянии h и отличную от прямой АВ;
• 4) Точку С на прямой b;
• 5) Прямые АС и ВС;
• 6) Точки D? a?АС и Е? a?ВС;
• 7) Прямые АЕ и ВD;
• 8) Точку P? АЕ?ВD;
• 9) Прямую СP;
• 10) Точку X? СP?АВ.

Так как DЕ — средняя линия треугольника АСВ, то АЕ и ВD — его медианы, а значит и СP — медиана, так что точка X искомая.

• 4. Прямым углом (рис. 27).
• 1) Строим прямую АВ;
• 2) Проводим прямые АА и ВВ', перпендикулярные прямой АВ;
• 3) Выбираем на АА' произвольную точку С, отличную от А;
• 4) Через точку С проводим СС' АС;
• 5) Точку D? СС'?ВВ';
• 6) Прямые АD и ВС;
• 7) Точку P? АD?ВС;
• 8) Прямую PP’АВ;
• 9) Точку X? PP'?АВ.

Рис. 27.

Точка X искомая.

Может оказаться, что какая-либо задача на построение имеет несколько решений, т. е. существует несколько различных фигур, удовлетворяющих всем условиям задачи.

Решить задачу на построение — значит найти все её решения.

Различия в положении на плоскости принимается или не принимается в расчет в зависимости от формулировки самой задачи на построение, а именно в зависимости от того, предусматривает или не предусматривает условие задачи определённое расположение искомой фигуры относительно каких-либо данных фигур.

Если условие задачи не предусматривает определённого расположения искомой фигуры относительно данных фигур, то условимся искать только все неравные между собой фигуры, удовлетворяющие условиям задачи.

Если условие задачи предусматривает определённое расположение искомой фигуры, то полное решение состоит в построении всех фигур, удовлетворяющих условию задачи (если такие фигуры существуют в конечном числе). При этом даже равные фигуры, но различно расположенные относительно данных фигур, рассматриваются как различные решения данной задачи.

Встречаются задачи, имеющие бесконечно много решений. Таковы, например, задачи: построить окружность данного радиуса, касающуюся данной прямой; построить прямую, касательную к данной окружности; построить окружность, проходящую через две данные точки. Такого рода задачи называют неопределёнными.

Решение неопределённой геометрической задачи ищется в своего рода параметрической форме. Указывается приём построения фигур, удовлетворяющих условиям задачи, причём эти фигуры определяются выбором положения одной или нескольких произвольных точек на некоторых данных или построенных фигурах. Эти точки играют роль «геометрических параметров». Задача считается решённой, если при всевозможных допустимых положениях произвольных точек возникают все фигуры, удовлетворяющие условиям задачи.

Может оказаться, что фигуры, обладающей указанными в задаче свойствами, вовсе не существует. Так, например, нельзя построить окружность, вписанную в данный прямоугольник, если он не является квадратом, нельзя построить общую касательную к двум концентрическим окружностям. Может случиться также, что решение задачи существует, но не может быть найдено данными средствами. Например, нельзя построить прямую, соединяющую две данные точки, располагая только циркулем, или провести окружность, проходящую через три данные точки, располагая только линейкой. Во всех этих случаях решить задачу на построение — значит доказать, что искомая фигура не существует или, соответственно, что она не может быть построена данными средствами.

Иногда задача не имеет решений потому, что на искомую фигуру наложено слишком много условий. Например, нельзя построить окружность, проходящую через четыре заданные точки, или построить треугольник, зная три его стороны и один из углов. Задачи такого рода называют переопределёнными. [19].