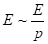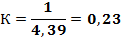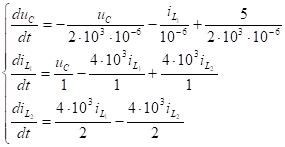Операторный метод. 
Переходные процессы в линейных электрических цепях

1. Определяются независимые начальные условия. Это токи в индуктивностях и напряжения на емкостях в момент времени t=0-.

А.

А.

В.

2. Находятся изображения источников.

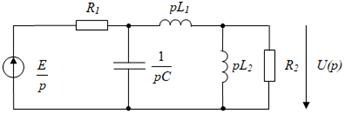
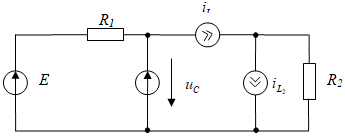
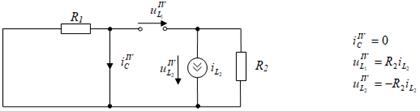
3. Составляется операторная схема замещения цепи после коммутации.

4. Выполняется расчет операторной схемы. Определяется изображение искомой величины.

линейный электрический цепь операторный.

5. Определяется оригинал искомой величины.

Метод переменных состояния

1. Составляется схема, в которой все источники напряжения заменяются на источники ЭДС, индуктивности — на источники тока, направленные по току, емкости — на источники ЭДС, направленные против напряжения.

• 2. Рассчитывается схема методом наложения. В качестве расчетных величин выступают все напряжения на индуктивностях и токи в конденсаторах.
• 1) действие источника E:

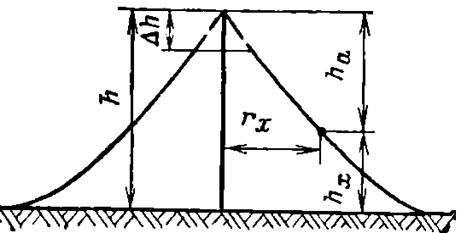
2) действие источника :

3) действие источника :

4) действие источника :

3. Составляется система дифференциальных уравнений.

Текст программы на MATLAB

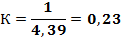
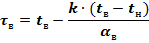
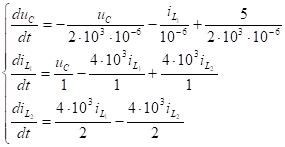
I_and_II_method.m.

clc;

clear all;

File=fopen ('Table.txt','wt');

fprintf (File,'%10s','t, ms','u, V');

fprintf (File,' ');

P=[1 6.5e3 4e6 2e9];

z=roots (P).

ti=0.002;

i=0;

t0=0;

tinc=0.1;

tmax=0.02;

for t=t0:tinc:tmax,.

i=i+1;

T (i)=t*1000;

u1(i)=0.32*exp (-5877.3*t)+(-0.32*cos (493.31*t)+3.61*sin (493.31*t))*exp (-311.34*t);

if t.

u2(i)=0;

else.

t1=t-ti;

u2(i)=-(0.32*exp (-5877.3*t1)+(-0.32*cos (493.31*t1)+3.61*sin (493.31*t1))*exp (-311.34*t1));

end;

u (i)=u1(i)+u2(i);

end;

plot (T, u1, T, u2, T, u), grid;

xlabel ('t, ms');

ylabel ('u, V');

legend ('u1,V','u2,V','u, V',-1);

[Str, Stl]=size (T);

for i=1:100:Stl,.

fprintf (File,'% 10.3f', T (i), u (i));

fprintf (File,' ');

end;

fclose (File);

III_method.m.

clc;

clear all;

y0=[0,0,0];

trange=0:0.1:20e-3;

[t, y]=ode23(@sisdu, trange, y0);

u1=4000*y (, 2)-4000*y (, 3);

plot (t*1000,u1), grid.

xlabel ('t, ms');

ylabel ('u1,V');

sisdu.m.

function CMO=sisdu (t, P).

y1=-500*P (1)-1e6*P (2)+2500;

y2=P (1)-4000*P (2)+4000*P (3);

y3=2000*P (2)-2000*P (3);

CMO=[y1;y2;y3];