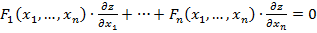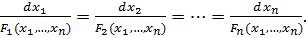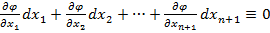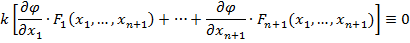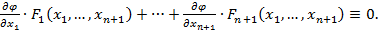Линейные дифференциальные уравнения в частных производных первого порядка
Для системы ОДУ определено понятие первого интеграла. В соответствие с ним под первым интегралом характеристической системы уравнения будем понимать отличную от константы непрерывно дифференцируемую в G функцию, которая на любой характеристике данного уравнения имеет постоянное значение: Необходимость. Легко проверить, что условие является не только необходимым, но и достаточным условием того… Читать ещё >
Линейные дифференциальные уравнения в частных производных первого порядка (реферат, курсовая, диплом, контрольная)
Определение.
Линейным однородным уравнением с частными производными первого порядка называется уравнение вида:
.
где — заданные функции, непрерывно дифференцируемые в рассматриваемой области G, — неизвестная функция.
Коэффициенты уравнения одновременно не обращаются в нуль ни в одной точке из G.
Решением уравнения будем называть непрерывно дифференцируемую в G функцию, обращающую равенство в тождество.
Геометрическое решение уравнения можно интерпретировать как некоторую гладкую n-мерную поверхность называемую интегральной поверхностью для данного уравнения.
Поставим в соответствие уравнению с частными производными систему обыкновенных дифференциальных уравнений, в симметрической форме записываемую в виде:
Такую систему ОДУ называют характеристической для уравнения, а ее решения (интегральные кривые) — характеристиками уравнения.
Характеристическая система удовлетворяет теореме существования и единственности решений, поэтому через каждую точку области G проходит единственная характеристика уравнения, в параметрической форме представимая в виде n функций:
Для системы ОДУ определено понятие первого интеграла. В соответствие с ним под первым интегралом характеристической системы уравнения будем понимать отличную от константы непрерывно дифференцируемую в G функцию, которая на любой характеристике данного уравнения имеет постоянное значение:
где С — константа.
Теорема 2. Функция является решением уравнения (2) тогда и только тогда, когда является первым интегралом системы.
Доказательство.
1) Достаточность (). Пусть имеется уравнение Очевидно, что уравнение определяет первый интеграл системы, тогда и только тогда, когда для любого ее решения :
Отсюда:
.
.
Но из (3) находим:
.
Следовательно:
.
Таким образом, функция является решением уравнения.
Необходимость. Легко проверить, что условие является не только необходимым, но и достаточным условием того, что уравнение определяет первый интеграл системы дифференциальных уравнений. Следовательно, если — решение уравнения, то уравнение определяет первый интеграл системы.