Примеры построения оценок

Пример 1.1: Оценка математического ожидания mx признака x в генеральной совокупности. Пусть X1, X2… X3 — предполагаемая выборка, по которой мы собираемся оценить mx. По соглашению математическое ожидание каждой компоненты Xt равно:

M (X1) = mx * (t = 1.2…n).

Т. е., каждая выборочная компонента может служить несмещенной оценкой неизвестной величины mx. Средняя выборочная так же будет несмещенной оценкой mx. Действительно, по свойствам математического ожидания:

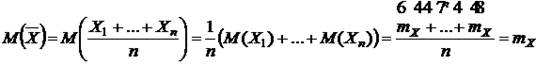
Рассмотрим далее свойство эффективности оценок. Для этого предположим, что найдено несколько несмещенных независимых оценок параметра mx, дисперсия каждой из которых D (X1), т. е., равна дисперсии признака X. Будем искать линейную комбинацию оценок X, удовлетворяющую условиям несмещенности и минимальности дисперсии параметра mx:

Из требования несмещенности:

В результате получаем задачу на условный экстремум для функции k переменных:

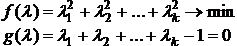
Для решения задачи по методу Лагранжа, составляем функцию:

Необходимые условия экстремума:

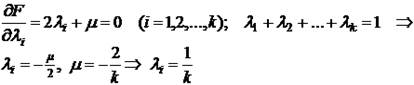
Так как:

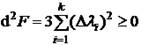
Тогда точка примет вид:

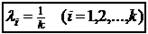
• — что является точкой условного минимума функции, т. е., оценка:
• — это имеет минимальную дисперсию при условии:

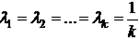
— при равной:

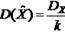
Применим теорему Чебышева:

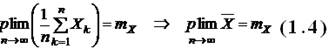
Отсюда следует, что оценка X является и состоятельной оценкой математического ожидания ГС.

Пример 1.2: Оценка дисперсии Dx признака X в генеральной совокупности. Как и в примере 1.1, рассмотрим оценку по формуле:

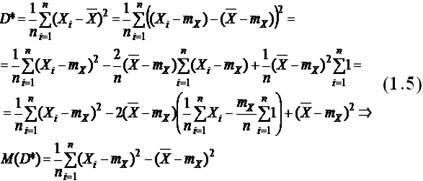
Для проверки несмещенности найдем математическое ожидание:

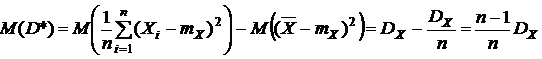
Таким образом, оценка генеральной дисперсии с помощью выборочной дисперсии является смещенной. Чтобы получить несмещенную оценку дисперсии, выборочную дисперсию следует умножить на поправочный коэффициент:

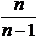
Т. е., вместо выборочной дисперсии D для оценки следует взять исправленную выборочную дисперсию:

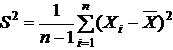
Для проверки состоятельности оценки D найдем предел по вероятности от правой части. Первое слагаемое:

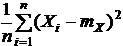
Является средним арифметическим n независимых, одинаково распределенных:

СВ * (X1 — mx)²

По закону больших чисел:

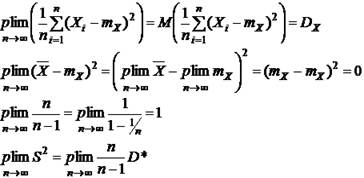
Т. е., исправленная дисперсия так же является состоятельной оценкой генеральной дисперсии.

Пример 1.3: Ковариация (корреляционный момент) между СВ X и Y определяется как математическое ожидание произведения СВ:

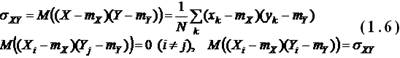
Покажем, что несмещенной оценкой ковариации является выборочный корреляционный момент:

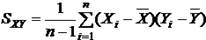
Предварительно преобразуем это выражение:

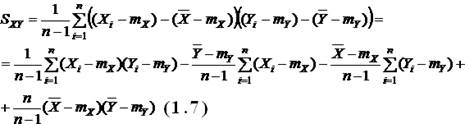
Заменяя:

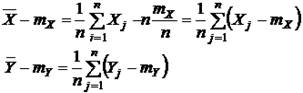
Получаем:

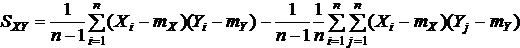
Так как в 1-й сумме n слагаемых, то математическое ожидание 1-й суммы равно:

Во второй сумме n2 слагаемых, причем для n из них (когда i=j) математическое ожидание равно xr.

А для остальных равно нулю. Тогда математическое ожидание 2-й суммы равно:

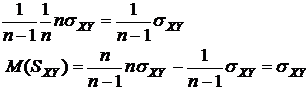
Т. е., Sxr является несмещенной оценкой для xr.

Состоятельность оценки Sxr доказывается точно таким же образом, как и состоятельность S2 при оценке дисперсии. Выражение:

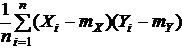
Является средним арифметическим n независимых, одинаково распределенных СВ:

По закону больших чисел:

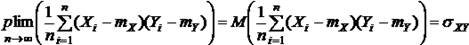
Предел по вероятности 1-й суммы «В» равен:

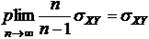
Пределы по вероятности остальных слагаемых в равны нулю.

Свойства оценок на основе МНК.

Возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров наиболее широко используется линейная функция.

В линейной множественной регрессии параметры при называются коэффициентами «чистой» регрессии.

Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Рассмотрим линейную модель множественной регрессии.

Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от расчетных минимальна.

Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю.

После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения параметров линейного уравнения множественной регрессии.

Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе.

Стандартизированные переменные для которых среднее значение равно нулю, а среднее квадратическое отклонение равно единице (стандартизированные коэффициенты регрессии).

Стандартизованные коэффициенты регрессии показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор изменится на одну единицу при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии можно сравнивать между собой.

Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.

Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений.

Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе к уравнению регрессии в натуральном масштабе переменных.

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов — из модели исключаются факторы с наименьшим значением.

На основе линейного уравнения множественной регрессии могут быть найдены частные уравнения регрессии: т. е., уравнения регрессии, которые связывают результативный признак с соответствующим фактором при закреплении остальных факторов на среднем уровне.

При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии.

В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне.

Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности, при которой коэффициент регрессии для фактора в уравнении множественной регрессии — частное уравнение регрессии.

Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности: которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.