Курс факультативных занятий для 9 класса

Будем доказывать, что треугольник не может занимать больше половины площади прямоугольной коробки. Для этого нам нужно рассмотреть все случаи расположения вершин, можем считать, что все вершины лежат на сторонах прямоугольника. «Либо на одной из сторон лежат две вершины треугольника — этот случай разобран под а), либо вершины треугольника лежат на трех сторонах, а точнее, на двух сторонах… Читать ещё >
Курс факультативных занятий для 9 класса (реферат, курсовая, диплом, контрольная)
Рабочая программа факультатива по геометрии «Площади фигур»
Пояснительная записка.
ОГЭ по математике является обязательным экзаменом в 9 классе. Работа состоит из двух частей с тремя модулями и содержит в себе 26 заданий. Так как в данной работе мы рассматриваем задания только по геометрии, задания по алгебре будем опускать. В первой части задания по геометрии идут с 9 по 13, где нужно дать краткий ответ, в части второй задания по геометрии расположены с 24 по 26, в которых нужно записать подробное решение с развернутым ответом. Чтобы набрать минимальный балл по математике нужно решить, помимо модуля «Математика», из модуля «Геометрия» не менее трех заданий. Так как геометрия является более сложной для изучения, создан данный факультативный курс.
Курс факультативных занятий «Площади фигур» разработан на основе следующих документов:
Федеральный компонент государственного стандарта общего образования, утвержденный приказом Минобразования РФ № 1089 от 09.03.2004 (с изменениями и дополнениями от 23. 06.2015 г.).
Федеральный базисный учебный план для среднего (полного) общего образования, утвержденный приказом Минобразования РФ № 1312 от 05.03.2004 (с изменениями и дополнениями от 01.02.2012 г.).
Федеральный перечень учебников, рекомендованных Министерством образования к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования, утвержденным приказом МО РФ № 1677 от 29.12.2016 г.
Факультативные занятия рекомендованы учащимся 9-х классов для развития их математического кругозора, приобретения умений и навыков при решении геометрических задач по теме «Площади фигур», предназначены для подготовки основного государственного экзамена.
Цель курса факультативных занятий — подготовка учащихся к продолжению образования, повышения уровня их математической культуры, подготовка к ОГЭ.
Задачи курса:
подготовить учащихся к ОГЭ;
учить высказывать гипотезы, опровергать их или доказывать;
развивать интуицию и умение предвидеть результаты работы;
помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их использования.
Курс рассчитан на 9 часов и предполагает компактное и четкое изложение теоретического материала, решение задач, самостоятельную работу.
Формы занятий:
беседа;
практические занятия;
работа в группах;
индивидуальные занятия;
тест ОГЭ как форма подведения итогов работы курса.
Содержание курса:
Тема № 1 «Площадь многоугольников».
Тема № 2 «Площадь треугольников».
Тема № 3 «Решение задач ОГЭ, нестандартных задач».
Тема № 4 «Площадь круга. Решение задач».
Тема № 5 «Итоговый урок».
Таблица 3.1 — Название.
№№. | Тема занятия. | Количество часов. | Форма занятия. | Оборудование. | |
| Площадь многоугольников. | Беседа. Работа в группах. | мультимедиа, чертежные инструменты. | ||
| Площадь треугольников. | Беседа. Работа в группах. | мультимедиа, чертежные инструменты. | ||
| Решение задач ОГЭ, нестандартных задач. | Практические занятия. Индивидуальные занятия. | мультимедиа. | ||
| Площадь круга. Решение задач. | Беседа. Работа в группах. Индивидуальные занятия. | мультимедиа. | ||
Итоговый урок. | Индивидуальные занятия. | мультимедиа. | |||
Содержание программы.
Тема 1. Площадь многоугольников.
В рамках данной темы рассматриваются задачи на нахождение площадей многоугольников. В начале проводится актуализация знаний, вспоминается понятие площади, единицы измерения, свойства площадей. Через решение задач вспоминаются формулы площадей многоугольников. По мимо задач ученики решают кроссворд по теме «Площади фигур», составляют интеллект — карту, что делает урок разнообразным и творческим. Затем дается формула Пика, с помощью которой ученики решают задание из ОГЭ. После делают выводы по уроку и записывают домашнее задание.
Некоторые из предлагаемых задач:
Задача 1.
Дан прямоугольник ABCD. На стороне AD этого прямоугольника построен треугольник ADE. Построен он так, что его стороны AE, DE пересекают отрезок BC в точках M и N. Точка M является серединой отрезка AE. Докажите, что .
Решение:
В данной задаче рассматриваются два треугольника ABM и MEO. (рис. 3.1) Они равны по второму признаку равенства треугольников. Это означает, что и другая пара треугольников NEO и DCN равны. Из этого следует, что .
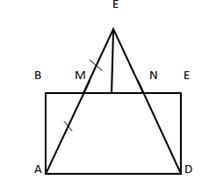
Рис. 3.1 Прямоугольник
Задача 2.
Площадь поверхности озера Байкал составляет 31 722. Выразите площадь в квадратных метрах и гектарах.
Ответ: 31 722 000 000; 3 172 200 гектар.
Тема 2. Площадь треугольников.
В рамках этой темы рассматриваются задачи на нахождение площади произвольного треугольника, нахождение площади треугольника через радиус вписанной и описанной окружности. Рассматривается формула Герона, площадь прямоугольного треугольника, площадь равностороннего треугольника, на данные темы решаются задачи. Урок представлен больше в практической части. Отрабатываются задания из ОГЭ.
Некоторые из предлагаемых задач:
Задача 1.
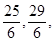
Найдите площадь треугольника по трем сторонам: а) 19,67,82; б) 6.
Ход решения:
Для того, чтобы решить эту задачу, нужно вспомнить формулу, по которой находится площадь треугольника. В данном случае рационально использовать формулу Герона., где.

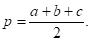
Задача 2.
Найдите площадь треугольника, если его стороны a и b, угол между ними .
а) а=6, b=8, =30б) а=14, b=5, =60.
Ход решения:
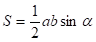
Как и в предыдущей задаче, запишем формулу площади треугольника по двум сторонам и углу между ними .
Тема 3. Решение задач ОГЭ, нестандартных задач.
Данная тема разделена на несколько уроков, так как важная часть геометрии — это отработка всей полученной теории на практике при решении задач. Ученики в ходе уроков решают задачи из ОГЭ. Далее учитель демонстрирует решение опорной задачи. Однако следует обратить внимание учащихся на то, что задачи внутри данной темы не являются стандартными, они более разнообразны по своему содержанию, что затрудняет работу по алгоритму уже решенной задачи и требует творческого подхода к каждому решению.
Некоторые из предлагаемых задач:
Задача 1.
Площадь равнобедренного прямоугольного треугольника составляет половину площади квадрата со стороной, равной катету. А какова площадь «пиксельного» (составленного из единичных квадратов) равнобедренного прямоугольного треугольника с катетом 20? (рис. 3.2 «Пиксельный» треугольник).
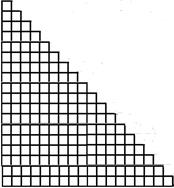
Рис. 3.2 «Пиксельный» треугольник
Решение задачи:
Первый способ. Если мы возьмем два таких треугольника, то из них можно получить прямоугольник с размером 20×21 (рис. 3.3 Прямоугольник).

Рис. 3.2 Прямоугольник

Соответственно, площадь треугольника в два раза меньше и равна .
Второй способ. Если рассмотреть обычный не пиксельный треугольник, то можно заметить, что он занимает половину коробки из-за симметрии. Это означает, что часть, которая не занята, симметрична занятой части. Будем рассуждать также для пиксельного треугольника. Если отразить его относительно диагонали, то исходный треугольник будет пересекаться с отраженным.(рис. 3.3 Отраженный треугольник).

Рис. 3.3 Отраженный треугольник
Но число клеток в пересечении нетрудно найти: все они лежат на диагонали квадрата и их ровно 20 штук. Получаем, что если искомая площадь равна S, то площадь квадрата равна S-20. То есть S.

Задача 2.
Треугольник при укладке в коробку перекосило а) Занимает ли он большую, меньшую, или такую же часть площади коробки? б) Можно ли положить треугольник площади 10 в прямоугольную коробку площади 19?(рис. 4 Треугольник).

Рис. 3.4 Треугольник
Рассмотрим решение данной задачи:
- а) Сторона треугольника, которая является самой длинной, делит коробку пополам. Но следует заметить, что треугольника занимает только часть половины коробки.
- б) Будем доказывать, что треугольник не может занимать больше половины площади прямоугольной коробки. Для этого нам нужно рассмотреть все случаи расположения вершин, можем считать, что все вершины лежат на сторонах прямоугольника. «Либо на одной из сторон лежат две вершины треугольника — этот случай разобран под а), либо вершины треугольника лежат на трех сторонах, а точнее, на двух сторонах и в углу (рис. 3.5 Треугольник 2)

Рис. 3.5 Треугольник 2
Тогда коробка разбивается на три части, в каждой из которых треугольник занимает не больше половины площади. (рис. 3.6 Треугольник 3).
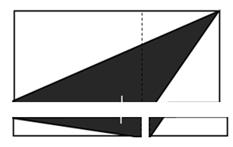
Рис. 3.6 Треугольник 3
Тема 4. Площадь круга. Решение задач.
На этом занятии ученики решают задачи на нахождение площади круга, сектора и сегмента. Тренируются на задачах с заштрихованной частью фигуры, для дальнейшего нахождения площади фигуры.
Некоторые из предлагаемых задач:
Задача 1.
Дано два круга, у которых радиусы по 6 см. Они имеют общую хорду длиной 6. Найдите площадь общей части данных кругов.
Решение :
В ходе решения мы пользуемся обратной теоремой Пифагора. Из него следует, что треугольник BOD прямоугольный, то есть .
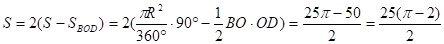
Тема 5 Итоговый урок.
На завершающем этапе каждому ученику даются тесты, которые в ходе урока он должен решить и получить за них баллы. Это будет являться оценкой усвоения данного факультативного курса.
Некоторые из предлагаемых задач:
Задача 1.
Найдите площадь трапеции, которая изображена на клетчатой бумаге (рис. 3.7 Трапеция).

Рис. 3.7 Трапеция
Ход решения:
Для решения подобных задач можно воспользоваться формулой Пика.
Задача 2.
Найдите площадь прямоугольника, если сторона его на 7 больше другой стороны и его периметр 72.
Решение:
Сначала нужно вспомнить площадь прямоугольника. Формула площади: S=ab. Составим уравнение, чтобы выразить через стороны периметр. Пусть x — меньшая сторона прямоугольника, тогда другая сторона будет равна x-7. Тогда периметр прямоугольника будет равен 2(x+x+7) = 72. Находим теперь x: 2x+2x+14=72. Из этого выходит, что x=14,5. Площадь прямоугольника равна 311,75.
Ответ: 311,75.