Математическая модель, построенная на основе мультисловарей

лингвистический словарь тезаурус терминологический Для второй модели в качестве входных параметров системы нечёткого вывода также будем рассматривать 6 нечётких лингвистических переменных (см. модель 1.). А в качестве выходных параметров — 3 нечеткие лингвистические переменные, определяющие принадлежность текста к предметной области: «Fuzzy» — F, «Logik» — L, «Mathematik» — M.

В качестве терм-множества всех лингвистических переменных (ЛП) будем использовать множество Т1={"min", «med», «max», «none"} (Рис.3). При этом каждый из термов ЛП будем оценивать по шкале от 0 до 1, при которой цифре 0 соответствует наименьшая принадлежность терминов текста к определенному подсловарю, а цифре 1 — наибольшая.

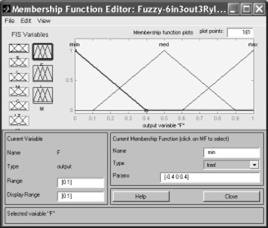
Рис. 3. Функции принадлежности выходной переменной F

После обработки 18 текстов по НЛ, 10 текстов по математике и 10 текстов по логике программой Fuzzy Base были получены частотные характеристики, на основе которых по средним значениям относительных частот встречаемости терминов построен частотный портрет (Рис. 4.). [Арзамасцева и др., 2008b].

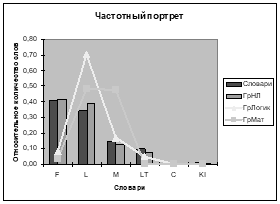
Рис. 4. Частотный портрет

Затем по данным усредненных частот групп текстов каждой предметной области были найдены минимальные и максимальные значения. (Табл.1.).

Табл. 1.

По данным этих усредненных частот были сформулированы 3 нечетких правила отнесения текста к предметной области Нечеткой логики, Математики и Логики (система нечёткого вывода типа Мамдани):

ПРАВИЛО 1: ЕСЛИ уровень относительной частоты терминов F в тексте — «средний» И уровень относительной частоты терминов L — «средний» И уровень относительной частоты терминов M — «минимальный» И уровень относительной частоты терминов LT — «минимальный» И термины словарей C и KI — отсутствуют, ТО степень уверенности, что текст принадлежит к предметной области F — максимальная.

ПРАВИЛО 2: ЕСЛИ уровень относительной частоты терминов F в тексте — «минимальный» И уровень относительной частоты терминов L — «максимальный» И уровень относительной частоты терминов M — «минимальный» И термины словарей C, LT и KI — отсутствуют, ТО степень уверенности, что текст принадлежит к предметной области L — максимальная.

ПРАВИЛО 3: ЕСЛИ уровень относительной частоты терминов F в тексте — «минимальный» И уровень относительной частоты терминов L — «средний» И уровень относительной частоты терминов M — «максимальный» И термины словарей C, LT и KI — отсутствуют, ТО степень уверенности, что текст принадлежит к предметной области М — максимальная.

Формализованное множество данных правил выглядит следующим образом:

R₁ — IF X₁ is «med» AND X₂ is «med» AND X₃ is «min» AND LT is «min» then Text is F.

R₂ — IF X₁ is «min» AND X₂ is «max» AND X₃ is «min» then Text is L.

R₂ — IF X₁ is «min» AND X₂ is «med» AND X₃ is «max» then Text is M.

В таблице 2 приведены эти 3 правила базы знаний, сформулированные на основе частотных портретов текстов.

Табл. 2.

Задача идентификации предметной области состоит в определении степени принадлежности определенного текста к предметной области НЛ на основе нечеткого вывода на базе построенной модели. Точность модели будем оценивать с помощью значения среднеквадратической невязки [Штовба, 2003].

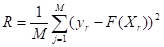
Где F (X) — значение выхода нечеткой модели при значении входов, заданных вектором X = [F, L, M, LT, C, KI], М — количество текстов, ? = 1 — степень уверенности принадлежности текста к предметной области НЛ.

На вход модели в качестве степени уверенности принадлежности терминов текста к соответствующему словарю подаются относительные частоты терминов всех подсловарей в каждом тексте.

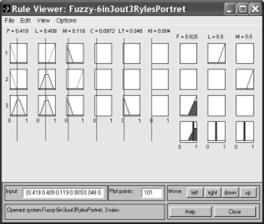
Рис. 5. Правила нечеткого вывода для вектора данных средних значений текстов по НЛ

Расчет выбранной оценки по первым десяти текстам представлен в таблице 3.

Табл. 3.

Математическая модель определения принадлежности текста предметной области на основе мультисловарей, построенная на базе нечеткого вывода по Мамдани:

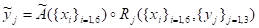
где.

? — нечеткая выходная переменная;

x — входная переменная;

i — индекс для входов;

j — индекс для выходов;

Г — функция принадлежности входных переменных {A₁, A_2, A_3, A_4, A_5, A₆};

R_k — множество правил.